Derivata

Multi tool use

In matematica, la derivata è la misura di quanto la crescita di una funzione cambi al variare del suo argomento.
La derivata di una funzione è una grandezza puntuale, cioè si calcola punto per punto. Nel caso di funzioni a una variabile nel campo reale, essa è la pendenza della tangente al grafico della funzione in quel punto e ne rappresenta la migliore approssimazione lineare. Nel caso in cui la derivata esista (cioè la funzione sia derivabile) in ogni punto del dominio, la si può vedere a sua volta come una funzione che associa a ogni punto proprio la derivata in quel punto.
Il concetto di derivata è, insieme a quello di integrale, uno dei cardini dell'analisi matematica e del calcolo infinitesimale.
Il significato pratico di derivata è il tasso di variazione di una certa grandezza presa in considerazione. Un esempio molto noto di derivata è la variazione della posizione di un oggetto rispetto al tempo, chiamata velocità istantanea.
Indice
1 Descrizione
2 Definizione
2.1 Derivata complessa
2.1.1 Relazione tra derivata reale e complessa
2.2 Derivata destra e derivata sinistra
2.3 Notazioni
2.4 Derivata parziale
2.5 Derivata direzionale
3 Generalizzazioni della derivata
4 Differenziabilità di una funzione
5 Continuità e derivabilità
5.1 Funzioni non derivabili
6 Teoremi
6.1 Regole di derivazione
6.2 Teorema di Fermat
6.3 Teorema di Rolle
6.4 Teorema di Lagrange
6.5 Teorema di Cauchy
6.6 Monotonia a partire dalla derivata
7 Derivate di ordine superiore
7.1 Convessità
8 Significato geometrico della derivata
9 Esempio
10 Note
11 Bibliografia
12 Voci correlate
13 Altri progetti
14 Collegamenti esterni
Descrizione |

La derivata di una funzione in un punto è il coefficiente angolare della retta tangente alla curva nel punto. Si tratta quindi di un numero che misura la pendenza della retta tangente.
La derivata di una funzione f{displaystyle f}




Nel caso di funzioni di più variabili la tangente in un punto alla curva della funzione non è unica, ma varia a seconda della direzione scelta. Non si può più quindi definire una sola funzione delle stesse variabili indipendenti che renda conto della pendenza del grafico della funzione in un punto: si ricorre allora alle derivate parziali della funzione, cioè ai coefficienti angolari di tangenti considerate lungo direzioni parallele agli assi che rappresentano le variabili indipendenti.
Le derivate parziali sono in numero pari alle variabili stesse, e una loro notevole proprietà è che se la funzione è sufficientemente "regolare" (cioè differenziabile) è possibile calcolarne la tangente lungo una direzione qualunque con una combinazione lineare delle derivate parziali stesse. Questo è possibile perché l'operatore di derivazione è un operatore lineare, e quindi la derivata di una combinazione lineare di funzioni derivabili è la combinazione lineare delle derivate delle singole funzioni, e la derivata del prodotto di uno scalare per una funzione è il prodotto dello scalare per la derivata della funzione.
Definizione |

Un'animazione che dà un'idea intuitiva della derivata, poiché lo "swing" di una funzione cambia quando cambia l'argomento.
La nozione di derivata si introduce, nel caso più semplice, considerando una funzione reale f(x){displaystyle f(x)}









- f′(x0)=limh→0f(x0+h)−f(x0)h{displaystyle f'(x_{0})=lim _{hto 0}{frac {f(x_{0}+h)-f(x_{0})}{h}}}
e il valore di questo limite è la derivata della funzione nel punto x0{displaystyle x_{0}}








Derivata complessa |
.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}
Nonostante il caso più semplice sia quello delle funzioni reali, la definizione di derivata trova la sua collocazione più naturale nell'ambito dell'analisi complessa, dove, applicata alle funzioni di variabile complessa, prende il nome di derivata complessa.[1] Detto U{displaystyle U}


- f′(z0)=limz→z0f(z)−f(z0)z−z0{displaystyle f'(z_{0})=lim _{zto z_{0}}{frac {f(z)-f(z_{0})}{z-z_{0}}}}
Tale limite va inteso in relazione alla topologia del piano. In altre parole, per ogni successione di numeri complessi che converge a z0{displaystyle z_{0}}




Relazione tra derivata reale e complessa |
La relazione tra la differenziabilità di funzioni reali e funzioni complesse è data dal fatto che se una funzione complessa:
- f(z)≡f(x+iy)=u(x,y)+iv(x,y){displaystyle f(z)equiv f(x+iy)=u(x,y)+i,v(x,y)}
è olomorfa allora u{displaystyle u}



- ∂u∂x=∂v∂y∂u∂y=−∂v∂x{displaystyle {frac {partial u}{partial x}}={frac {partial v}{partial y}}qquad {frac {partial u}{partial y}}=-{frac {partial v}{partial x}},}
In modo equivalente, la derivata di Wirtinger ∂f/∂z¯{displaystyle partial f/partial {overline {z}}}



Derivata destra e derivata sinistra |
La derivata destra di f{displaystyle f}

- f+′(x0)=limh→0+f(x0+h)−f(x0)h{displaystyle f'_{+}(x_{0})=lim _{hto 0^{+}}{frac {f(x_{0}+h)-f(x_{0})}{h}}}
Analogamente, la derivata sinistra di f{displaystyle f}

- f−′(x0)=limh→0−f(x0+h)−f(x0)h{displaystyle f'_{-}(x_{0})=lim _{hto 0^{-}}{frac {f(x_{0}+h)-f(x_{0})}{h}}}
Una funzione è derivabile in x0{displaystyle x_{0}}

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![x in [a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)


Notazioni |
La prima notazione di derivata nel punto x0 che compare storicamente è:
- (dfdx)(x0){displaystyle left({frac {mathrm {d} f}{mathrm {d} x}}right)_{(x_{0})}}
ancora oggi usata in fisica. In alternativa, secondo la notazione di Lagrange viene indicata con:
- f′(x0){displaystyle f^{prime }(x_{0})}
secondo la notazione di Cauchy - Eulero con:
- D[f(x0)]{displaystyle operatorname {D} left[{f}({x_{0}})right]}
secondo la notazione di Leibniz con:
- df(x0)dx{displaystyle {frac {mathrm {d} f(x_{0})}{mathrm {d} x}}}
e secondo la notazione di Newton con:
- f˙(x0){displaystyle {dot {f}}(x_{0})}
Derivata parziale |
Nel caso di una funzione di più variabili, l'incremento della funzione rispetto a una sola variabile è la derivata parziale della funzione rispetto a tale variabile. Data una funzione vettoriale di più variabili F:E⊂Rn→Rm{displaystyle mathbf {F} :Esubset mathbb {R} ^{n}rightarrow mathbb {R} ^{m}}





- F(x)=∑imFi(x)uix=(x1,x2,…,xn)∈E{displaystyle mathbf {F} (mathbf {x} )=sum _{i}^{m}F_{i}(mathbf {x} )mathbf {u} _{i}quad mathbf {x} =(x_{1},x_{2},dots ,x_{n})in E}
La componente i-esima della funzione è allora:
- Fi(x)=F(x)⋅ui1≤i≤m{displaystyle F_{i}(mathbf {x} )=mathbf {F} (mathbf {x} )cdot mathbf {u} _{i}quad 1leq ileq m}
Si definisce derivata parziale di Fi{displaystyle F_{i}}

- ∂Fi(x)∂xj=limt→0Fi(x+tej)−Fi(x)t=limt→0Fi(x1,x2,…xj+t,…,xn)−Fi(x1,x2,…,xn)t{displaystyle {begin{aligned}{frac {partial F_{i}(mathbf {x} )}{partial x_{j}}}&=lim _{tto 0}{frac {F_{i}(mathbf {x} +tmathbf {e} _{j})-F_{i}(mathbf {x} )}{t}}\&=lim _{tto 0}{frac {F_{i}(x_{1},x_{2},ldots x_{j}+t,ldots ,x_{n})-F_{i}(x_{1},x_{2},ldots ,x_{n})}{t}}end{aligned}}}
Tale limite è a volte chiamato limite del rapporto incrementale di f{displaystyle f}


Derivata direzionale |
La derivata direzionale di una funzione scalare f(x)=f(x1,x2,…,xn){displaystyle f(mathbf {x} )=f(x_{1},x_{2},ldots ,x_{n})}

- Duf(x)=limh→0+f(x+hu)−f(x)h{displaystyle D_{mathbf {u} }{f}(mathbf {x} )=lim _{hrightarrow 0^{+}}{frac {f(mathbf {x} +hmathbf {u} )-f(mathbf {x} )}{h}}}
Se la funzione f{displaystyle f}


- Duf(x)=∇f(x)⋅u{displaystyle D_{mathbf {u} }{f}(mathbf {x} )=nabla f(mathbf {x} )cdot mathbf {u} }
dove ∇f{displaystyle nabla f}






Generalizzazioni della derivata |
Differenziabilità di una funzione |

Una funzione da R{displaystyle mathbb {R} }
 in R{displaystyle mathbb {R} }
in R{displaystyle mathbb {R} } è derivabile in un punto se è approssimabile vicino a quel punto da una retta. Tale retta deve quindi essere tangente al grafico della funzione. Questa nozione si estende in dimensioni arbitrarie, e prende il nome di funzione differenziabile.
è derivabile in un punto se è approssimabile vicino a quel punto da una retta. Tale retta deve quindi essere tangente al grafico della funzione. Questa nozione si estende in dimensioni arbitrarie, e prende il nome di funzione differenziabile.Una funzione differenziabile in un punto è una funzione che può essere approssimata da una trasformazione lineare nel punto. Affinché ciò si verifichi è necessario che tutte le derivate parziali calcolate nel punto esistano, ovvero esistono finiti i limiti dei rapporti incrementali direzionali (dunque, se una funzione è differenziabile in un punto allora è derivabile nel punto). La proprietà di differenziabilità di una funzione consente di generalizzare il concetto di funzione derivabile a funzioni vettoriali di variabile vettoriale, e permette di individuare per ogni punto del suo grafico un iperpiano tangente.
Una funzione F:U→Rm{displaystyle mathbf {F} :Urightarrow mathbb {R} ^{m}}



- F(x0+h)−F(x0)=L(x0)h+r(h){displaystyle mathbf {F} (mathbf {x} _{0}+mathbf {h} )-mathbf {F} (mathbf {x} _{0})=mathbf {L} (mathbf {x} _{0})mathbf {h} +mathbf {r} (mathbf {h} )}
dove r(h){displaystyle mathbf {r} (mathbf {h} )}

- limh→0F(x0+h)−F(x0)−L(x0)h‖h‖=0{displaystyle lim _{mathbf {h} to mathbf {0} }{frac {mathbf {F} (mathbf {x} _{0}+mathbf {h} )-mathbf {F} (mathbf {x} _{0})-mathbf {L} (mathbf {x} _{0})mathbf {h} }{|mathbf {h} |}}=mathbf {0} }
Se la funzione F{displaystyle mathbf {F} }



Il vettore:
- L(x0)h=dF(x0)=JFh{displaystyle mathbf {L} (mathbf {x} _{0})mathbf {h} =mathrm {d} mathbf {F} (mathbf {x} _{0})=J_{F}mathbf {h} }
si chiama differenziale di F{displaystyle mathbf {F} }



La funzione F{displaystyle mathbf {F} }


Continuità e derivabilità |
Il teorema di continuità asserisce che se f(x){displaystyle f(x)}



L'inverso non è sempre vero: ad esempio, la funzione f(x)=|x|{displaystyle f(x)=|x|}



- f(x)={0 se x∈Qx2 se x∈R∖Q{displaystyle f(x)={begin{cases}0{text{ se }}xin mathbb {Q} \x^{2}{text{ se }}xin mathbb {R} setminus mathbb {Q} end{cases}}}
essendo Q{displaystyle mathbb {Q} }

Per mostrare che se f(x){displaystyle f(x)}


- f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0){displaystyle f(x)=f(x_{0})+f^{prime }(x_{0})(x-x_{0})+o(x-x_{0})}
da cui:
- limx→x0f(x)=limx→x0f(x0)+f′(x0)(x−x0)+o(x−x0)=f(x0){displaystyle {begin{aligned}lim _{xto x_{0}}f(x)&=lim _{xto x_{0}}f(x_{0})+f^{prime }(x_{0})(x-x_{0})+o(x-x_{0})\&=f(x_{0})\end{aligned}}}
Quindi la funzione è continua in x0{displaystyle x_{0}}

- f(x)=f(x0)+o(1){displaystyle f(x)=f(x_{0})+o(1)}
garantita dalla sola continuità (qui o(1)⟶x→x00{displaystyle o(1){underset {xto x_{0}}{longrightarrow }}0}



- f(x)=f(x0)+f′(ξ)(x−x0){displaystyle f(x)=f(x_{0})+f^{prime }(xi )(x-x_{0})}
per tutti gli x{displaystyle x}




Funzioni non derivabili |

La funzione valore assoluto non è derivabile nell'origine, dove ha un punto angoloso
Una funzione continua può essere non derivabile. Ad esempio, una funzione continua può non essere derivabile in un punto isolato del dominio, in presenza di un punto angoloso, una cuspide o un flesso a tangente verticale. Esistono anche funzioni continue che presentano forme più complesse di non derivabilità, come ad esempio la funzione di Cantor. La funzione di Weierstrass è una funzione reale di variabile reale che ha la proprietà di essere continua in ogni punto ma di non essere derivabile in nessuno.
Teoremi |
Vengono enunciati di seguito alcuni teoremi e risultati significativi.
Regole di derivazione |
Siano f(x){displaystyle f(x)}




- D[f(x)]=f′(x)D[g(x)]=g′(x){displaystyle mathrm {D} [f(x)]=f'(x)qquad mathrm {D} [g(x)]=g'(x)}
Regola della somma (linearità):
- D[αf(x)+βg(x)]=αf′(x)+βg′(x)α,β∈R{displaystyle mathrm {D} [alpha f(x)+beta g(x)]=alpha f'(x)+beta g'(x)qquad alpha ,beta in mathbb {R} }
Regola del prodotto (o di Leibniz):
- D[f(x)⋅g(x)]=f′(x)⋅g(x)+f(x)⋅g′(x){displaystyle mathrm {D} [{f(x)cdot g(x)}]=f'(x)cdot g(x)+f(x)cdot g'(x)}
Regola del quoziente:
- D[f(x)g(x)]=f′(x)⋅g(x)−f(x)⋅g′(x)g(x)2{displaystyle mathrm {D} !left[{f(x) over g(x)}right]={f'(x)cdot g(x)-f(x)cdot g'(x) over g(x)^{2}}}
Regola della funzione reciproca:
- D[1f(x)]=−f′(x)f(x)2{displaystyle mathrm {D} !left[{1 over f(x)}right]=-{f'(x) over f(x)^{2}}}
Regola della funzione inversa:
- D[f−1(y)]=1f′(x){displaystyle mathrm {D} [f^{-1}(y)]={1 over f'(x)}}
- con:
- y=f(x)x=f−1(y){displaystyle y={f(x)}qquad x={f^{-1}(y)}}
Regola della catena:
- D[f(g(x))]=f′(g(x))⋅g′(x){displaystyle mathrm {D} left[fleft(g(x)right)right]=f'left(g(x)right)cdot g'(x)}
Teorema di Fermat |
Sia f(x){displaystyle f(x)}





Non è indispensabile che x0{displaystyle x_{0}}



Questo teorema è molto usato nello studio di funzione, in quanto definisce la possibilità di avere un punto di massimo o di minimo dove la funzione derivata si annulla.
Teorema di Rolle |
Sia f(x){displaystyle f(x)}
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




Teorema di Lagrange |
Sia f(x){displaystyle f(x)}
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


- f′(x0)=f(b)−f(a)b−a{displaystyle f'(x_{0})={{f(b)-f(a)} over {b-a}}}
Il teorema afferma che esiste almeno un punto (x0,f(x0)){displaystyle (x_{0},f(x_{0}))}




Teorema di Cauchy |
Siano f(x){displaystyle f(x)}

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



- f′(x0)g′(x0)=f(b)−f(a)g(b)−g(a){displaystyle {f'(x_{0}) over g'(x_{0})}={{f(b)-f(a)} over {g(b)-g(a)}}}
Considerando in particolare la funzione g(t)=t{displaystyle g(t)=t}
Con il teorema di Cauchy è inoltre possibile dimostrare la regola di de l'Hôpital.
Monotonia a partire dalla derivata |
Sia f(x){displaystyle f(x)}
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

- Per ogni x∈(a,b){displaystyle xin (a,b)}
si ha f′(x)⩾0{displaystyle f'(x)geqslant 0}
se e solo se la funzione è crescente in (a,b){displaystyle (a,b)}
.
- Per ogni x∈(a,b){displaystyle xin (a,b)}
si ha f′(x)⩽0{displaystyle f'(x)leqslant 0}
se e solo se la funzione è decrescente in (a,b){displaystyle (a,b)}
.
La funzione può non essere strettamente crescente (o decrescente), e il teorema è direttamente ricavabile dall'enunciato di Lagrange.
Analogamente, valgono anche i fatti seguenti:
- Se per ogni x∈(a,b){displaystyle xin (a,b)}
si ha f′(x)>0{displaystyle f'(x)>0}
allora la funzione è strettamente crescente in (a,b){displaystyle (a,b)}
.
- Se per ogni x∈(a,b){displaystyle xin (a,b)}
si ha f′(x)<0{displaystyle f'(x)<0}
allora la funzione è strettamente decrescente in (a,b){displaystyle (a,b)}
.
Una funzione strettamente crescente non ha necessariamente derivata ovunque positiva. Ad esempio, f(x)=x3{displaystyle f(x)=x^{3}}
Il teorema della funzione costante afferma che una funzione è costante in un intervallo [a,b]{displaystyle [a,b]}![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
Derivate di ordine superiore |
La derivata n-esima f(n){displaystyle f^{(n)}}



- f″=f(2)=d2fdx2f‴=f(3)=d3fdx3⋮f(n)=dnfdxn{displaystyle {begin{aligned}f''=f^{(2)}&={frac {mathrm {d} ^{2}f}{mathrm {d} x^{2}}}\f'''=f^{(3)}&={frac {mathrm {d} ^{3}f}{mathrm {d} x^{3}}}\&vdots \f^{(n)}&={frac {mathrm {d} ^{n}f}{mathrm {d} x^{n}}}end{aligned}}}
Una funzione derivabile non è necessariamente derivabile n{displaystyle n}



La classe delle funzioni derivabili n{displaystyle n}


Convessità |
Sia f:[a,b]→R{displaystyle f:[a,b]to mathbb {R} }![f: [a,b] to mathbb{R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)


![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

- f″(x)≥0{displaystyle f''(x)geq 0}
Il cambiamento di segno della derivata seconda determina quindi un cambiamento di convessità della funzione e un relativo punto di flesso.
Significato geometrico della derivata |
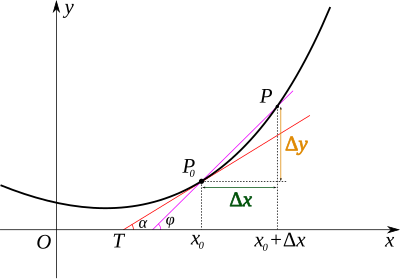
La retta in rosso è la tangente al grafico della f(x) nel punto (x0, f(x0))
Il valore della derivata di f(x){displaystyle f(x)}




L'equazione della retta tangente in x0{displaystyle x_{0}}
- y=f(x0)+f′(x0)(x−x0) {displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}) }
Più precisamente, se f(x){displaystyle f(x)}



- f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0){displaystyle f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})}
con:
- limx→x0o(x−x0)x−x0=0{displaystyle lim _{xto x_{0}}{{o(x-x_{0})} over {x-x_{0}}}=0}
e tale formula è l'espansione di Taylor di f(x){displaystyle f(x)}






Se si definisce infatti o(x−x0){displaystyle o(x-x_{0})}

- o(x−x0)=f(x)−f(x0)−f′(x0)(x−x0){displaystyle o(x-x_{0})=f(x)-f(x_{0})-f^{prime }(x_{0})(x-x_{0})}
si verifica che:
- limx→x0o(x−x0)x−x0=limx→x0(f(x)−f(x0)x−x0−f′(x0)){displaystyle lim _{xto x_{0}}{{o(x-x_{0})} over {x-x_{0}}}=lim _{xto x_{0}}left({frac {f(x)-f(x_{0})}{x-x_{0}}}-f^{prime }(x_{0})right)}
Ricordando che per x→x0{displaystyle xto x_{0}}


- limh→0f(x0+h)−f(x0)h−f′(x0)=0{displaystyle lim _{hto 0}{frac {f(x_{0}+h)-f(x_{0})}{h}}-f^{prime }(x_{0})=0}
Esempio |
Una funzione espressa come serie di potenze ∑n=0∞anXn{displaystyle sum _{n=0}^{infty }a_{n}X^{n}}


- f′(x)=∑n=1∞nanxn−1{displaystyle f'(x)=sum _{n=1}^{infty }na_{n}x^{n-1}}
Tuttavia, in una serie di potenze si preferisce che n{displaystyle n}
- f′(x)=∑n=0∞(n+1)an+1xn{displaystyle f'(x)=sum _{n=0}^{infty }{(n+1)}a_{n+1}x^{n}}
Questo tipo di derivata è importante per lo sviluppo di Taylor e Mc-Laurin.
Note |
^ Weisstein, Eric W. Derivative. From MathWorld, su mathworld.wolfram.com. URL consultato il 25-11-2012.
^ Rowland, Todd. Complex Differentiable. From MathWorld, su mathworld.wolfram.com. URL consultato il 25-11-2012.
^ Weisstein, Eric W. Cauchy-Riemann Equations. From MathWorld, su mathworld.wolfram.com. URL consultato il 25-11-2012.
^ W. Rudin, Pag. 216.
^ W. Rudin, Pag. 219.
^ W. Rudin, Pag. 214.
^ W. Rudin, Pag. 220.
Bibliografia |
Paolo Marcellini, Carlo Sbordone Analisi Matematica Uno, Liguori Editore, Napoli, ISBN 88-207-2819-2, 1998.
Nicola Fusco, Paolo Marcellini, Carlo Sbordone Analisi Matematica Due, Liguori Editore, Napoli, ISBN 88-207-2675-0, 1996.- Walter Rudin, Principi di Analisi Matematica, Milano, McGraw-Hill, 1991, ISBN 88-386-0647-1.
- (EN) Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 11, 1972.
- (EN) Amend, B. Camp FoxTrot. Kansas City, MO: Andrews McMeel, p. 19, 1998.
- (EN) Anton, H. Calculus: A New Horizon, 6th ed. New York: Wiley, 1999.
- (EN) Beyer, W. H. Derivatives. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 229–232, 19
Voci correlate |
- Approssimazione lineare
- Classe C di una funzione
- Derivata mista
- Derivata parziale
- Derivata direzionale
- Derivata simmetrica
- Derivata totale
- Derivazione complessa
- Funzione differenziabile
- Funzione olomorfa
- Generalizzazioni della derivata
- Gradiente
- Integrale
- Matrice jacobiana
- Notazione per la differenziazione
- Rapporto incrementale
- Regole di derivazione
- Sviluppo di Taylor
Altri progetti |
Altri progetti
- Wikibooks
- Wikizionario
- Wikiversità
- Wikimedia Commons
 Wikibooks contiene testi o manuali su derivata
Wikibooks contiene testi o manuali su derivata
 Wikizionario contiene il lemma di dizionario «derivata»
Wikizionario contiene il lemma di dizionario «derivata»
 Wikiversità contiene lezioni su derivata
Wikiversità contiene lezioni su derivata
 Wikimedia Commons contiene immagini o altri file su derivata
Wikimedia Commons contiene immagini o altri file su derivata
Collegamenti esterni |
- Derivata, in Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana, 15 marzo 2011.
WIMS Function Calculator calcolo delle derivate online; questo sito permette anche di fare esercizi interattivi- Differenziazione calcolatrice, su easycalculation.com.
- (EN) Online Derivatives Calculator.
Limite, derivate, integrali Directory con varie risorse sulle derivate
Derivata, su Treccani.it, Istituto dell'Enciclopedia Italiana.
Derivata, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
(EN) Derivata, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}
KAz21TVCUUtuI13wf4xN4Dn0x aeIzR2zkr








![operatorname D left[{f}({x_0})right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51c000bd32ba39e29e922b447f16063d41be0b3d)















![mathrm{D}[f(x)]=f'(x) qquad mathrm{D}[g(x)]=g'(x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23dcfb30d20a2a13440fb9f6acafe22b918d3f2)
![mathrm{D}[alpha f(x)+ beta g(x)] = alpha f'(x) + beta g'(x) qquad alpha, beta in R](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb55be1bd258890bd1e05085b54350de1dd9282f)
![mathrm{D} [ {f(x) cdot g(x)}] = f'(x) cdot g(x) + f(x) cdot g'(x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc918c90195d7cb3b3cec94f7271fc141ac020eb)
![mathrm{D}! left[ {f(x) over g(x)} right] = { f'(x) cdot g(x) - f(x) cdot g'(x) over g(x)^2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a848c2328d398ba22ae09e72a1124fecd966d1d6)
![mathrm{D}! left[ {1 over f(x)} right] = -{f'(x) over f(x)^2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e717492ec466809feddcedb08422e943d7341ab)
![mathrm{D}[f^{-1}(y)] = {1 over f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/484c45781e1de88ba7f1745c6994c20b1094c2e7)

![mathrm{D} left[ f left( g(x) right) right] = f' left( g(x) right) cdot g'(x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6612d72dfc0b1b0e1ab50ce666d502ddefa57dd)












