Gfrktyl

Un magnete che levita sopra un superconduttore ad alta temperatura, raffreddato con azoto liquido, la levitazione avviene grazie all'effetto Meissner-Ochsenfeld.

La superconduttività è un fenomeno fisico che comporta resistenza elettrica nulla ed espulsione del campo magnetico, esso avviene in alcuni materiali al di sotto di una caratteristica temperatura detta critica. Tale proprietà fu scoperta per la prima volta nel 1911 da Heike Kamerlingh Onnes,^[1]. Come il ferromagnetismo e le linee spettrali atomiche tale fenomeno non è spiegabile
mediante la fisica classica, ma solo mediante la meccanica quantistica.

L'effetto Meissner-Ochsenfeld, cioè il fatto che alcuni
materiali espellono il campo magnetico presente al loro interno quando al diminuire della temperatura passano nello stato superconduttore, indica che la superconduttività non può essere spiegata come un perfetto conduttore della fisica classica. Un perfetto conduttore classico espelle per la legge di Faraday un campo magnetico se improvvisamente aumenta il flusso concatenato, ma l'espulsione del campo magnetico da parte di un superconduttore può avvenire anche se il flusso concatenato non varia e cambia la temperatura passando il materiale dallo stato normale a quello superconduttore.

La resistenza elettrica di un conduttore metallico diminuisce gradualmente al diminuire della temperatura. Ma nei metalli comuni, come ad esempio
il rame o l'argento, al di sotto di una certa temperatura, che dipende dalle impurità e dai difetti, la resistenza non varia più. Quindi anche vicino allo
zero di assoluto i conduttori presentano una resistenza elettrica. Il fatto rilevante nei superconduttori è che la resistenza si annulla completamente, quando il materiale è raffreddato al di sotto della sua temperatura detta critica. Quindi una corrente elettrica può scorrere indefinitamente in un circuito chiuso senza nessun generatore che lo alimenti
^[2].

Nel 1986, si è scoperto che un cuprato ceramico con struttura della perovskite aveva una temperatura critica di 40 K (−233 °C)^[3]. Pochi mesi dopo venne annunciato che un composto di YBa₂Cu₃O₇ ha una temperatura critica di 93 K (−180 °C)^[4]. Da queste due scoperte inizia una nuova linea di ricerca in ogni parte del mondo, scoprendo anno dopo anno nuovi e interessanti materiali. Bisogna aggiungere che ottenere materiali superconduttori a temperatura ambiente attualmente sembra una utopia.

Tali alte temperature sono impossibili da raggiungere con i superconduttori tradizionali, per cui questi materiali sono chiamati superconduttori ad alta temperatura critica.
L'azoto liquido che bolle a 77 K, è un fluido criogenico economico e di largo uso che permette una facile sperimentazione di tali materiali.

Classificazione |

Ci sono vari criteri con cui possono essere classificati i superconduttori, i più comuni sono:

Risposta al campo magnetico |

Un superconduttore si dice del

• I tipo: se ha un solo campo critico, cioè un campo magnetico al di sopra del quale la superconduttività è persa e al di sotto del quale il campo magnetico è completamente espulso.


• II tipo: se vi sono due campi critici: al di sotto del primo campo critico il campo è completamente espulso, tra il primo ed il secondo campo critico vi una parziale penetrazione del campo magnetico. Il campo entra sotto forma di vortici quantizzati.


• Tipo 1,5: se in superconduttori con molte componenti è possibile avere la combinazione di entrambi i due tipi di comportamento.

Dal modello teorico |

• 
  Convenzionale: se il comportamento viene spiegato con la teoria BCS.


• 
  Non convenzionale: se il comportamento non viene spiegato con la teoria BCS. Sono state proposte molte teorie, ma non c'è ancora una teoria valida accettata da tutta la comunità scientifica.

Dalla temperatura critica |

• Alta temperatura: se la temperatura critica è maggiore di quella dell'azoto liquido T_c > 77 K.


• Bassa temperatura: se la temperatura critica è inferiore a T_c < 77 K.

Dal tipo di materiale |

Le classificazioni dii materiali in questo caso possono essere:

• 
  elementi ad esempio niobio o piombo
  


• 
  leghe come Niobio titanio, niobio germanio o nitruro di Niobio
  


• 
  ceramiche come l'YBCO o il diboruro di magnesio (MgB₂)


• Superconduttori a base di ferro come il LaOFeAs drogato con fluoro


• Superconduttori organici come i fullereni o i nanotubi di carbonio che potrebbero essere anche messi nella categoria elementi, essendo composti di solo carbonio.

Storia |

Heike Kamerlingh Onnes (a destra) riceve la visita di (da sinistra a destra) Paul Ehrenfest, Hendrik Lorentz, Niels Bohr .

Il fenomeno della superconduttività fu scoperto nel mercurio nel 1911 dal fisico olandese Heike Kamerlingh Onnes,^[1] a temperature criogeniche utilizzando l'elio prodotto già pochi anni prima in forma liquida. La liquefazione dell'elio fu il fatto rilevante per cui ricevette il premio Nobel per la fisica nel 1913. Egli trovò che alla temperatura di 4.2 K, la resistenza del mercurio si annullava.
Nello stesso esperimento, egli trovò anche la transizione superfluida dell'elio a 2.2 K, però non ne capì l'importanza. Solo cento anni dopo riesaminando i quaderni di laboratorio fu ricostruito il fatto^[5]. Negli anni successivi la superconduttività fu osservata in molti altri materiali. Nel 1913 fu trovato che anche il piombo era superconduttore a 7 K. Kamerlingh Onnes si illuse di potere fare un magnete con piombo producendo un campo magnetico di 10 T, ma riuscì a fare solo campi di 60 mT. La svolta sui magneti iniziò quando solo nel 1941 si trovarono i primi superconduttori del II tipo. Il primo fu il nitruro di Niobio che era superconduttore a 16 K ed in seguito altre leghe.

Grandi sforzi vennero fatti negli anni successivi per trovare il come e il perché della superconduttività; un passo importante fu quando Meissner e Ochsenfeld scoprirono che i superconduttori espellevano il campo magnetico, un fenomeno che è ora conosciuto come effetto Meissner^[6].
Nel 1935 i fratelli Fritz e Heinz London mostrarono che l'effetto Meissner è una conseguenza della minimizzazione della energia libera di Gibbs^[7]. La teoria che è sintetizzata da due equazioni dette le equazioni di London, il successo della teoria è proprio nella spiegazione dell'effetto Meissner.

Nel 1950, contemporaneamente Maxwell e Reynold (assieme a dei collaboratori) trovarono che la temperatura critica è proporzionale alla radice massa isotopica del mercurio
^[8][9]. Questa importante risultato sperimentale mise in luce per la prima volta l'importanza della interazione fonone-elettrone per spiegare il meccanismo microscopico della superconduttività.

Solo nel 1955 viene fatto il primo piccolo magnete di 0.7 T, fatto da un avvolgimento di Niobio titanio, una lega ancora attualmente utilizzata in quasi tutti i magneti^[10].

Durante il decennio del 1950, lo sviluppo teorico dellafisica della materia condensata è riuscito a spiegare in maniera soddisfacente il comportamento dei superconduttori convenzionali attraverso due approcci diversi prima nel 1950 con la teoria di Ginzburg-Landau e in seguito nel 1957 con la teoria BCS. La teoria di Ginzburg–Landau fu formulata da Landau e Ginzburg^[11]. Questa toeria mette insieme la teoria di Landau delle transizioni di fase del secondo ordine con un'equazione simile a quella di Schrödinger. Questa teoria spiega molte delle proprietà macroscopiche. In particolare Abrikosov ha mostrato come la teoria di Ginsburg-Landau prevede la divisione dei superconduttori in due tipi che ora sono chiamati superconduttori del I e II tipo. Abrikosov e Ginzburg nel 2003 hanno ricevuto il premio Nobel per la fisica per tale lavoro (Landau lo aveva ricevuto nel 1962 per altri lavori ed era morto nel 1968). L'estensione a quattro dimensioni della teoria di Ginsburg-Landau va sotto il nome di modello di Coleman-Weinberg ed è importante in teoria quantistica dei campi e in cosmologia.

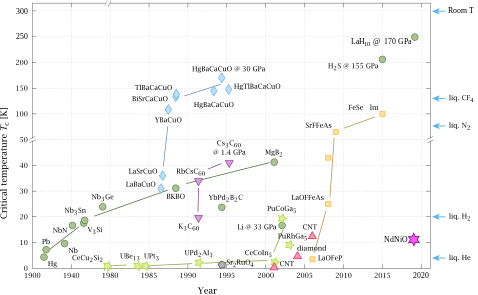
Storia dei vari materiali superconduttori

Una teoria microscopica completa della superconduttività fu infine proposta nel 1957 da Bardeen, Cooper and Schrieffer, tale teoria è detta BCS (dalle loro iniziali)^[12]. La teoria BCS spiega la corrente superconduttrice come dovuta a un superfluido fatto di coppie di Cooper, coppie di elettroni che si attraggono attraverso lo scambio di fononi. L'importanza di questo lavoro valse agli autori il premio Nobel per la fisica del 1972.

La teoria BCS fu perfezionata nel 1958 quando Bogolyubov mostrò che la funzione d'onda della teoria BCS che era stata ricavata mediante metodi variazionali, poteva essere ottenuta mediante una trasformazione canonica della Hamiltoniana elettronica
^[13]. Nel 1959 Gork'ov mostrò che la teoria BCS si riduceva alla teoria di Ginsburg-Landau nelle vicinanze della temperatura critica^[14][15]. La generalizzazione della teoria BCS per i superconduttori convenzionale forma la base per la comprensione della superfluidità, avendo la transizione molte caratteristiche simili all'elio-4_superfluido. I superconduttori non convenzionali non riescono a essere descritti da questo modello.

Nel 1961 Doll e Nabauer^[16] verificarono la quantizzazione del flusso magnetico. Cioè data un anello superconduttore il flusso magnetico concatenato può assumere solo multipli interi del quanto di flusso Φo=h/2e=2,067⋅10−15 Wb{displaystyle Phi _{o}=h/2e=2,067cdot 10^{-15} Wb}. La quantizzazione era stata prevista nel 1948 da F. London^[17], ma con un valore due volte maggiore.

Nel 1962 B. Josephson previde^[18] che una supercorrente poteva scorrere tra due superconduttori separati da un sottile isolante. Questo fenomeno attualmente è chiamato effetto Josephson. Questa scoperta assieme alla quantizzazione del flusso magnetico permisero nel 1964 di realizzare i primi SQUID^[19].

Nel 1973 viene trovato che il Nb₃Ge ha una temperatura di 23 K, tale valore rimase la più alta temperatura in un superconduttore per 13 anni.

Nel 1986 K. A. Müller e J. G. Bednorz scoprirono che una ceramica di bario, lantanio, rame e ossigeno diventa superconduttrice alla temperatura di circa 35 K (−238 °C), temperatura significativamente maggiore dei 23 K (−250 °C) della migliore lega superconduttrice allora nota. Anche Müller e Bednorz ricevettero il premio Nobel per la fisica nel 1987.

Ulteriori ricerche hanno portato alla scoperta di ceramiche, sempre contenenti rame e ossigeno, tali da permettere di usare l'azoto liquido (alla temperatura di 77 K (−196 °C)) come refrigerante, molto più economico ed efficiente dell'elio. Una temperatura critica tanto alta suggerì la possibile esistenza di un superconduttore a temperatura ambiente, che da allora ha attirato e continua ad attirare in questo settore della fisica molti investimenti economici e l'interesse di molti ricercatori in tutto il mondo.

Nel 1993 è stato scoperto un superconduttore con una temperatura critica più alta, T_c 138 K (−135 °C); è un composto ceramico a base di mercurio, bario, calcio, rame e ossigeno,
(HgBa₂Ca₂Cu₃O_8+δ) ottenuto per sostituzione del tallio.^[20].
Ma recentemente si è trovato che il solfuro di idrogeno ha una temperatura critica di 203.5 K^[21].

Proprietà elementari |

La maggior parte delle proprietà dei superconduttori, quali temperatura critica, calore specifico, campo magnetico critico e densità di corrente critica, variano da materiale a materiale.

Mentre vi sono delle proprietà che sono indipendenti dal materiale: infatti tutti i superconduttori hanno esattamente una resistenza nulla se sono attraversati da una piccola corrente e il campo magnetico presente è debole. Inoltre come tutte le transizioni di fase ha delle proprietà universali che non dipendono dai dettagli microscopici del materiale.

Resistenza nulla |

Sezione di un tipico cavo superconduttore.

Il metodo più semplice di misura una resistenza elettrica su un campione di materiale è di metterlo in serie in un circuito elettrico in cui è presente un generatore di corrente. Se la differenza di potenziale ai campi del campione è zero, la resistenza è nulla. Per potere fare la misura è necessario avere quattro fili: due per la corrente e due per la tensione.

Quindi nei superconduttori la corrente continua a circolare anche se non è applicata nessuna differenza di potenziale. Tale proprietà è utilizzata nei magneti superconduttori che sono diffusamente usati nella tomografia a risonanza magnetica (MRI).
Gli esperimenti hanno dimostrato che la corrente può rimanere costante anche in un tempo di 100 mila anni, ma le stime teoriche prevedono che le correnti potrebbero avere una durata paragonabile all'età dell'Universo, ovviamente se la geometria è opportuna e la temperatura è mantenuta costante
^[22]. In pratica correnti iniettate in bobine superconduttrici sono rimaste immutate per più di 22 anni [1]^[23]. In questo esperimento, per la misura della accelerazione di gravità viene fatta usando la levitazione di una sfera di niobio di 4 grammi.

Nei conduttori normali, la corrente elettrica si comporta come un fluido di elettroni che si muovono in un reticolo di ioni molto più pesanti.
Nelle collisioni degli elettroni con gli ioni del reticolo viene dissipata parte dell'energia degli elettroni e ciò causa un riscaldamento del reticolo (effetto Joule). Maggiore è la resistenza elettrica maggiore è l'energia dissipata a parità di corrente.

La situazione è differente in un superconduttore. Nei superconduttori convenzionali, il fluido che trasporta la corrente elettrica è costituita non da elettroni, ma da coppie di elettroni le coppie di Cooper. L'accoppiamento è dato dal fatto che gli elettroni si scambiano dei fononi che determinano una attrazione tra di loro. In realtà la spiegazione è possibile solo mediante la meccanica quantistica che considera le coppie di Cooper un condensato di Bose-Einstein con una banda proibita, cioè esiste una minima quantità di energia ΔE{displaystyle Delta E} che deve essere fornita per potere eccitare il fluido di coppie. Perciò se ΔE{displaystyle Delta E} è maggiore dell'energia termica kBT{displaystyle k_{B}T} (dove kB{displaystyle k_{B}} è la costante di Boltzmann e T la tempertura), il fluido non viene alterato nel suo fluire nel reticolo. In realtà le coppie di Cooper si comportano come un superfluido, cioè un fluido che non dissipa energia.

Nei superconduttori del II tipo, tra cui i superconduttori ad alta temperatura, una piccolissima ma non nulla resistenza si manifesta al di sotto della transizione superconduttiva quando la corrente che scorre viene applicata assieme ad un campo magnetico intenso (che può essere anche causato dalla corrente stessa). La resistenza in questo caso è dovuta ai vortici nel reticolo di Abrikosov che muovendosi causano una dissipazione della energia portata dalla corrente. La resistenza elettrica dovuta a questo effetto è in genere molto inferiore a quella dei materiali non superconduttori. Correnti molto piccole non riescono a muovere i vortici e quindi non si ha resistenza, inoltre quando si va a temperatura bassa in genere i difetti nel reticolo dovuti anche a impurezze congelano i vortici che formano una struttura disordinata simile ad un vetro, al di sotto della temperatura di vetrificazione la resistenza del materiale si annulla. Il congelamento dei vortici permette ad alcuni superconduttori del II tipo di essere attraversati da correnti molto elevate e generare quindi campi molto intensi anche di alcune decine di Tesla.

Transizione di fase superconduttrice |

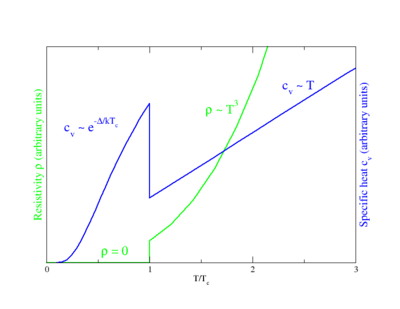
Comportamento della capacità termica (c_v, blu) e della resistività (ρ, verde) nella transizione di fase superconduttrice

Nei materiali superconduttori, la caratteristica della superconduttività appare quando la temperatura è portata al di sotto della temperatura critica T_c. Il valore della temperatura critica varia da materiale a materiale. I materiali convenzionali hanno temperature che vanno
da 23 K ( niobio germanio) fino a 15 mK (tungsteno), ma vi sono materiali con temperature critiche ancora più basse. In realtà tra i materiali convenzionali bisognerebbe includere anche il diboruro di magnesio(MgB₂) che ha una temperatura critica di 39 K
^[24]. Alcuni hanno dei dubbi sul definire superconduttore convenzionale il diboruro di magnesio in quanto ha delle proprietà esotiche rispetto agli altri materiali convenzionali.

I superconduttori non convenzionali possono avere temperature critiche molto maggiori. Ad esempio l'YBa₂Cu₃O₇, uno dei primi superconduttori scoperti contenente rame , ha una temperatura critica di 92 K,
La spiegazione del fatto che la temperatura critica possa essere così alta rimane una incognita. Infatti l'accoppiamento degli elettroni mediante fononi mentre spiega bene la superconduttività nei materiali convenzionali, non riesce a spiegare la superconduttività dei materiali non convenzionali, specialmente la temperatura così alta.

Inoltre al di sotto della temperatura critica, un materiale smette di supercondurre se viene applicati un campo magnetico maggiore del campo magnetico critico. Questo in quanto l'energia libera di Gibbs della fase superconduttrice cresce con il quadrato del campo magnetico, mentre l'energia libera di Gibbs della fase normale è una funzione abbastanza indipendente dal campo magnetico. La ragione per cui un materiale va nello stato superconduttore è che in assenza di campo magnetico la fase superconduttrice ha una energia libera minore della fase normale: ma all'aumentare del campo magnetico vi sarà un valore del campo per cui le due energie libere diventano eguali, al di sopra di tale campo la fase normale è quella
stabile. Una temperatura più alta ed un campo magnetico più intenso riducono le coppie di Cooper e di conseguenza aumenta la lunghezza di penetrazione di London, che diventa infinita alla transizione di fase. La lunghezza di penetrazione è proporzionale all'inverso della radice quadrata della densità delle coppie di Cooper.

La comparsa delle superconduttività è accompagnata da un cambiamento improvviso di varie proprietà fisiche, questa è una caratteristica delle
transizioni di fase, per esempio il calore specifico mentre nei metalli normali è una funzione lineare della temperatura, alla transizione superconduttrice ha un salto discontinuo e cessa di essere lineare. A temperatura lontana dalla transizione, varia con una legge del tipo e^−α/T con α una costante (con le dimensioni di una temperatura). Il comportamento esponenziale è una chiara prova dell'esistenza di una banda proibita.

Quale sia l'ordine della transizione di fase superconduttrice è una questione molto discussa. Gli esperimenti trovano che la transizione è del secondo ordine, in quanto non vi è un calore latente. Tuttavia, in presenza di un campo magnetico vi è un calore latente, poiché la fase superconduttrice ha una entropia più bassa della fase normale al di sotto della temperatura critica.
Infatti è stato dimostrato sperimentalmente che quando viene aumentato il campo magnetico al di sopra del campo critico, si ha una transizione di fase con una diminuzione della temperatura del materiale che era superconduttore^[25].

Nel 1970 sono stati fatti dei conti che hanno suggerito che le fluttuazioni a grande distanza del campo elettromagnetico possono dare luogo a una debole transizione del primo ordine. Nel 1980 è stato mostrato teoricamente, considerando il ruolo dei vortici nei superconduttori, che la transizione è del secondo ordine nei superconduttori del II tipo e del primo ordine (quindi con calore latente) nei superconduttori del I tipo. Le due regioni sono separate da un punto tricritico cioè un punto in cui termina la coesistenza di tre fasi^[26]. Questo risultato analitico è stato dimostrato numericamente mediante simulazione Monte Carlo^[27]

Effetto Meissner |

Rappresentazione dell'effetto Meissner: (a sinistra) a temperatura maggiore di T_c (stato normale) il materiale è attraversato da linee di forza del campo magnetico; (a destra) a temperatura minore di T_c (stato superconduttivo) il campo è espulso

Lo stesso argomento in dettaglio: Effetto Meissner.

Quando un materiale che diventa superconduttore è posto in un debole campo magnetico esterno B, e raffreddato al di sotto della sua temperatura di transizione, il campo magnetico è espulso, cioè un superconduttore è un diamagnete perfetto. L'effetto Meissner non causa la completa espulsione del campo magnetico, in quanto il campo penetra all'interno per una breve profondità, caratterizzata da λ la lunghezza di penetrazione di London, cioè detta z{displaystyle z,} la distanza dalla superficie esterna, il campo diminuisce esponenzialmente con la distanza dalla superficie.
Per la maggior parte dei superconduttori la lunghezza di penetrazione è dell'ordine di 100 nm.
Questo effetto permette la levitazione magnetica dei superconduttori.

L'effetto Meissner non può essere confuso con il diamagnetismo per un conduttore elettrico perfetto. Infatti per la legge di Faraday, quando un campo magnetico variabile è applicato ad un conduttore, esso induce una corrente elettrica nel conduttore che tende ad annullare il campo applicato. Se il conduttore è perfetto il campo magnetico è perfettamente cancellato. L'espulsione del campo magnetico da un superconduttore avviene non solo se poniamo un superconduttore in un campo magnetico, ma anche se viene utilizzato un campo magnetico costante e si varia la temperatura del materiale facendogli attraversare la transizione superconduttrice: secondo la legge di Faraday non vi è variazione del flusso concatenato e non vi sono correnti indotte.

Dell'effetto Meissner fu data una spiegazione dai due fratelli Fritz e Heinz London che proposero due equazioni fenomenologiche per descrivere la superconduttività, e da quella che è detta la II equazione di London si ricava utilizzando la Legge_di_Ampère:

∇2B→=B→λ2{displaystyle nabla ^{2}{vec {B}}={frac {vec {B}}{lambda ^{2}}}}

La cui soluzione è proprio:

B→(z)=B→(0)e−z/λ{displaystyle {vec {B}}(z)={vec {B}}(0)e^{-z/lambda }}

Un superconduttore in cui non vi è campo magnetico o ve ne è uno trascurabile si dice che si trova nello stato di Meissner. Quando viene applicato un campo molto intenso si ha la rottura dello stato Meissner, tale rottura avviene, in funzione della geometria prima del campo critico con regioni macroscopiche che rimangono senza campo (quindi superconduttrici) ed altre con campo magnetico (normale) tale stato viene chiamato lo stadio intermedio^[28], la struttura di tale stato è molto variegata^[29].
Nel caso dei superconduttori del II tipo, se il campo applicato supera il primo campo critico, lo stato diventa misto, è caratterizzato dalla formazione di vortici magnetici detti vortici di Abrikosov
^[30] quando viene posto in un campo magnetico.
La densità dei vortici aumenta all'aumentare dell'intensità del campo. A un campo magnetico ancora maggiore secondo campo critico la superconduttività è distrutta. La maggior parte degli elementi eccetto il niobio e i nanotubi di carbonio sono del I tipo, mentre tutte le leghe e i materiali compositi sono superconduttori del II tipo.

Momento di London |

Un oggetto superconduttore che ruota attorno al proprio asse, genera il campo di un momento magnetico: è il fenomeno reciproco dell'effetto Meissner.
Nell'esperimento Gravity Probe B si sono utilizzati dei giroscopi superconduttori costituite da delle sfere senza difetti fatte ruotare attorno ad un proprio asse la direzione di rotazione è stata misurata proprio grazie al momento di London mediante alcuni dc-SQUID.

Maggiori dettagli sulla classificazione magnetica |

I Tipo |

I superconduttori di primo tipo (solitamente metalli e alcune leghe metalliche) presentano una temperatura critica T_c molto bassa ed un'espulsione completa del campo magnetico dovuta a correnti superficiali indotte di intensità tale da generare fenomeni magnetici uguali e opposti al campo esterno, ottenendo così un campo magnetico interno al superconduttore teoricamente nullo (o praticamente trascurabile).

La superconduzione di tipo 1 si ritiene si realizzi per l'appaiamento degli elettroni in coppie, dette coppie di Cooper, che per effetti quantistici assumono un comportamento superfluido e quindi scorrono senza collisioni e senza produrre resistenza in alcuni conduttori al di sotto di una determinata temperatura, detta temperatura critica di superconduzione, T_c .

II Tipo |

Lo stesso argomento in dettaglio: Superconduttività del II tipo.

I superconduttori di secondo tipo (Niobio, Vanadio) presentano T_c molto più alte e sono caratterizzati dalla presenza di due valori critici per il campo magnetico. Oltre ad un primo valore di intensità B₁ (solitamente molto basso) il materiale è penetrato da linee di flusso del campo magnetico (flussoidi) distribuite ordinatamente al suo interno in un reticolo esagonale (stato misto, o di Abrikosov). All'aumentare dell'intensità del campo magnetico, il numero di flussoidi aumenta fino a portare alla distruzione della superconduttività ad un'intensità B₂ normalmente molto più alta rispetto ai valori di campo critico per superconduttori di primo tipo.

La superconduzione di tipo 2 è analoga a quella di tipo 1, e si realizza in conduttori detti "ad alta temperatura" (convenzionalmente superiore ai 20 K (−253 °C)); tali superconduttori, pur conservando una condizione di superconduzione, quando la temperatura si eleva a valori prossimi a quella di transizione alla conduzione classica, in presenza di forti flussi elettrici di superconduzione, presentano una resistenza al flusso estremamente piccola ma rilevabile, e che si incrementa mano a mano che ci si avvicina alla temperatura di transizione stessa. Si ritiene che tale minima resistenza sia dovuta all'induzione di una condizione di "vorticosità" del superfluido che produrrebbe il debole "attrito"; tale vorticosità sarebbe causata da una minima parziale penetrazione del campo magnetico all'interno del superconduttore.

Con correnti elettriche sufficientemente basse, o con riduzioni del campo magnetico, la resistenza svanisce, e quindi le presunte vorticosità sarebbero stabilizzate. Ugualmente con l'abbassamento della temperatura e l'allontanamento dal punto di transizione, la resistenza scende realmente a zero, quindi l'abbassamento della temperatura sembra annullare l'entità della presunta vorticosità.

Tipo 1,5 |

Ricercatori dell'University of Massachusetts Amherst e del Sveriges Största Tekniska Universitet hanno presentato una teoria che prevede l'esistenza di superconduttori in stato 1.5 su materiali chiamati superconduttori multibanda^[31], e che permette ai fisici di calcolare le condizioni necessarie per la loro riproducibilità: stabilità termodinamica, condizioni di repulsione a breve distanza, ordine di grandezza della penetrazione del campo magnetico minore di almeno un ordine rispetto a quello della variazione di densità dei corpi^[32]. Nei superconduttori di tipo 1.5, si formano a bassi campi magnetici due vortici con flussi simili, entrambi in uno stato di Meissner a due componenti: questi interagiscono con attrazione a lunga distanza dove prevale la forza fra le due densità, e con repulsione a breve distanza dove prevale l'interazione elettromagnetica.

Per anni la comunità scientifica ha ritenuto che esistessero solo superconduttori di tipo I o di tipo II, e che le due condizioni si escludessero a vicenda, senza ulteriori stati intermedi^[31].

Il fisico Babaev aveva però predetto l'esistenza di superconduttori di tipo 1.5, in cui gli elettroni avrebbero dovuto dividersi in due sottogruppi: uno che si comportava come i superconduttori di tipo I e l'altro di tipo II.

Fra le obiezioni vi era quella che comunque si trattava di elettroni, per cui era difficile accettare che, nello stesso superconduttore e condizioni esterne, potessero comportarsi in due modi così diversi (e ritenuti antagonisti)^[31].

Il dibattito era pure legato alla mancanza di una teoria che legasse la superconduttività alle proprietà su scale micro dei materiali.

Materiali superconduttori |

Lo stesso argomento in dettaglio: Lista di superconduttori.

Di seguito sono riportate le temperature critiche di elementi chimici puri:

• 
  gallio - T_c=1,1 K


• 
  alluminio - T_c=1,2 K


• 
  indio - T_c=3,4 K


• 
  stagno - T_c=3,7 K


• 
  mercurio - T_c=4,2 K


• 
  piombo - T_c=7,2 K


• 
  niobio - T_c=9,3 K

Di maggiore interesse sono i numerosi composti metallici superconduttori (ad esempio il niobio-stagno, T_c=17.9 K, e il magnesio-diboruro, T_c=39 K) e vari composti ceramici le cui temperature critiche possono superare i 120 K (−153 °C). Fra i composti ternari, quaternari o a più elementi maggiormente sintetizzati ed indagati vanno citate le ossopnictidi.
Attualmente il materiale conosciuto con la più alta temperatura critica è il Seleniuro di Ferro che a pressione normale (circa 1 kPa) è superconduttore fino a circa 30 K e, in linea teorica, a pressioni superiori ai 12,5 GPa, tale materiale dovrebbe avere una temperatura critica di circa 48 K. Perché tale materiale possa essere utilizzato per applicazioni pratiche è necessario però spingere la sua temperatura di transizione alla superconduttività a circa 77 K (la temperatura a cui bolle l'azoto liquido) e sembra che ciò sia possibile in quanto, facendo crescere un cristallo di Seleniuro di Ferro su un sottostrato di Titanato di Stronzio è stato rilevato un drastico aumento della temperatura di transizione del materiale.

Teoria della superconduzione |

Lo stesso argomento in dettaglio: Teoria BCS.

La teoria generalmente accettata come spiegazione di tale fenomeno, nota come teoria BCS, dalle iniziali dei tre fisici che l'hanno proposta (Bardeen, Cooper, Schrieffer), spiega il fenomeno come dovuto alle interazioni degli elettroni col reticolo cristallino, risultanti in un effetto netto di attrazione tra gli elettroni con spin opposti. Essi formano delle coppie, dette coppie di Cooper, che si comportano come una particella di spin 0. Tutte le particelle di spin 0 sono bosoni, al pari dei fotoni, e tendono a raggrupparsi in un unico stato quantistico, con ampiezza di probabilità proporzionale a n{displaystyle {sqrt {n}}}, dove n è il numero di particelle nello stesso stato.

La probabilità che una tale coppia sia distrutta dai moti termici obbedisce alla distribuzione di Maxwell-Boltzmann, ed è quindi proporzionale a e−EcoppiakT{displaystyle e^{-{frac {E_{coppia}}{kT}}}}.

L'energia di legame di queste coppie è normalmente molto bassa, tanto che per metalli normali bastano temperature di pochi kelvin per romperle. Quando però si è al di sotto della temperatura critica, ecco che tutte le coppie di elettroni hanno lo stesso stato quantistico, e sono dunque indistinguibili. Ora, dato che questi sono gli effetti netti dell'interazione tra elettroni e reticolo cristallino, in pratica è come se il reticolo non ci fosse, e si avesse una corrente libera di elettroni, che fluisce senza resistenza da parte del reticolo.

Poiché l'energia di legame è piccola, la distanza tra gli elettroni in una coppia è ampia, tanto da superare la distanza media tra le stesse coppie. Non tutti gli elettroni liberi formano coppie, e il numero degli elettroni normali sarà tanto maggiore quanto più la T è vicina alla temperatura di superconduzione.

Consideriamo il caso a temperatura pressoché nulla, per semplicità. Dato che la maggior parte delle particelle si trova nello stato a più bassa energia, ben presto la maggior parte degli elettroni converge nello stato di coppia non eccitata. In condizioni simili, detta ψ la funzione d'onda, la densità di probabilità delle particelle nello stato descritto dall'equazione è proporzionale a ψψ^* (o |ψ|²). Se includiamo la costante di proporzionalità entro la funzione, possiamo assumere il prodotto come la densità di carica ρ. In un superconduttore, così come in un conduttore, la ρ si può considerare costante.

Si può dunque riscrivere il tutto in coordinate polari (r, θ) come

ψ(r→)=ρ(r→)eiθ(r→){displaystyle psi ({vec {r}})={sqrt {rho ({vec {r}})}},e^{itheta ({vec {r}})}}

dove il secondo termine è un fattore di fase.
La legge di conservazione locale della probabilità impone che se la densità di probabilità P in una certa regione varia col tempo, ci deve essere un flusso: la particella non deve scomparire per riapparire altrove, ma deve muoversi con continuità. Questa non è nient'altro che una forma del teorema di Gauss, e quindi

∂P∂t=−∇⋅J→{displaystyle {frac {partial P}{partial t}}=-nabla cdot {vec {J}}}

e cioè la derivata temporale della densità di carica è pari all'opposto della divergenza della corrente.
Applicando la regola della derivata del prodotto a ψψ^*, sostituendo dapprima l'equazione di Schrödinger per una particella di massa m e carica q, in un potenziale V e potenziale vettore A

−ℏi∂ψ∂t=12m(ℏi∇−qA→)⋅(ℏi∇−qA→)ψ+qVψ{displaystyle -{frac {hbar }{i}}{frac {partial psi }{partial t}}={frac {1}{2m}}left({frac {hbar }{i}}nabla -q{vec {A}}right)cdot left({frac {hbar }{i}}nabla -q{vec {A}}right)psi +qVpsi }

e poi facendo il cambio in coordinate polari, si ottiene

(1)     J→=ℏm(∇θ−qℏA→)ρ{displaystyle {vec {J}}={frac {hbar }{m}}left(nabla theta -{frac {q}{hbar }}{vec {A}}right)rho }

Considerando che J non è altro che ρ per il vettore velocità v, si può ottenere

mv→=ℏ∇θ−qA→{displaystyle m{vec {v}}=hbar nabla theta -q{vec {A}}}

Applicazioni |

Un uso tipico dei superconduttori è per costruire bobine di magneti: l'uso di cavi superconduttori ne riduce di molto le dimensioni, il peso e il consumo di energia a parità di intensità di campo magnetico. Ovviamente la costruzione e il funzionamento di un magnete superconduttore è molto più costosa, richiedendo che sia mantenuto ad una temperatura inferiore a quella critica. Una tipica applicazione di questo tipo riguarda la realizzazione dei grandi toroidi dei sistemi clinici di risonanza magnetica nucleare.

I superconduttori sono stati usati in condizioni sperimentali anche su grande scala in grandi macchine come gli acceleratori del CERN, sono stai utilizzati in cavi conduttori del LEP e attualmente nell'LHC dove è necessario avere campi magnetici molto intensi (circa 9 T).

Questo ha permesso di evitare enormi dimensioni delle parti che ne sarebbero derivate, ridurre ovviamente la dispersione ohmica, ed ottenere altissime densità di corrente e di campo magnetico necessarie per gli esperimenti, in tale caso si sono adottati sia superconduttori che supermagneti.

Potenzialmente gli sviluppi possibili sono enormi in campi come accumulazione e trasmissione di energia, motori elettrici e realizzazione di grandi campi magnetici.

È da notare peraltro che la superconduzione, in senso generale, è discretamente controllata e ben gestibile solo con correnti continue "pulite". La maggior parte degli utilizzi tecnologici attuali di potenza si hanno con correnti variabili o alternate; tali correnti inducono nei campi magnetici ampie variazioni, alle quali lo stato di superconduzione è particolarmente sensibile.

Riproduci file multimediale

Animazione di levitazione magnetica tramite superconduttore

Con particolari configurazioni di giunzioni a materiale superconduttore si possono inoltre creare nuovi dispositivi, basati sulle giunzioni Josephson, formate da due superconduttori separati da un isolante. L'estrema sensibilità, la precisione e la velocità di transizione per la presenza di campi elettro-magnetici è utilizzata in questi dispositivi per dare misure estremamente precise di tali campi, o per ottenere commutazioni localizzate alla superconduzione (o dalla superconduzione a quella normale) estremamente sensibili e veloci; data la natura nanometrica (e quantistica) del dispositivo i tempi di commutazione sono estremamente brevi, dell'ordine dei picosecondi.

Ad esempio, le giunzioni sono utilizzate nella realizzazione di dispositivi per la misura del campo magnetico (SQUID) capaci di misurare valori infinitesimi di campo magnetico ed usati, anche in ambito medico, per alcuni tipi di analisi.

Queste giunzioni sono sfruttate anche in rivelatori di particelle per rivelare piccolissimi cambiamenti di temperatura causati dall'interazione con la particella da rivelare. Quando una particella attraversa il rivelatore, gli cede energia che causa un aumento di temperatura. Misurando la variazione di resistenza del rivelatore, che viene mantenuto in prossimità della temperatura critica, si può rilevare quando una particella attraversa il sensore.

Il superisolamento |

Lo stesso argomento in dettaglio: superisolamento.

Nell'aprile del 2008 giunse notizia della scoperta all'Argonne National Laboratory (USA) da parte dei fisici Valerii Vikonur e Tatyana Baturina, con la collaborazione di altri europei, del fenomeno del superisolamento.
Un sottile strato di nitruro di titanio sottoposto a raffreddamento ha mostrato, raggiunta la temperatura critica, una caduta di circa 100 000 volte nella sua capacità di conduzione. Le modalità di transizione al nuovo stato sembrano simili a quella della superconduzione, come ad esempio la sensibilità alla presenza di un campo magnetico^[33].

Note |

Bibliografia |

• (EN) J. R. Schrieffer. Theory of Superconductivity (Frontiers in Physics). New York, Benjamin-Cummings Publishing Company, 1988. ISBN 978-0-8053-8501-4
  


• (EN) M. Tinkham. Introduction to Superconductivity. New York, Dover, 2005. ISBN 0-486-43503-2
  


• (EN) A. Barone, G. Paternò. Physics and Applications of the Josephson Effect. New York, John Wiley & Sons, 1982.


• (EN) J. C. Gallop, the Josephson Effects and Superconducting Electronics, CRC Press, 1990, ISBN 0-7503-0051-5
  


• (EN) P. G. de Gennes. Superconductivity of metals and alloys. New York, W. A. Benjamin, Inc., 1966


• (EN) R. D. Parks. Superconductivity. CRC Press, 1969 ISBN 0-8247-1520-9
  


• (EN) G Rickayzen. Theory of Superconductivity. New York, Wiley-Interscience, 1965.


• (EN) J. Bardeen, L. Cooper, J. R. Schriffer Theory of Superconductivity (1957) ristampato da N. N. Bogoliubov (1963), Vol. 4, CRC Press, ISBN 0677000804
  


• L. Landau, E. Lifsits, L. Pitaevskij. Fisica Teorica 8: Elettrodinamica dei mezzi continui. Roma, Editori Riuniti, 1978. (effetto Meissner)


• L. Landau, E. Lifsits, L. Pitaevskij. Fisica Teorica 9: Fisica statistica. Roma, Editori Riuniti, 1981. (teoria di Ginzburg-Landau e teoria BCS)

Voci correlate |

• Teoria di Ginzburg-Landau


• Teoria BCS


• Effetto Meissner


• Equazioni di London


• Effetto isotopico (superconduttore)


• Superfluidità


• Quantizzazione del flusso


• Induttanza cinetica


• Superconduttività del II tipo


• Elettromagnetismo


• Superconduttività del colore SU(2)


• Large Hadron Collider


• Conducibilità elettrica


• Metalli

Altri progetti |

• 
  Wikimedia Commons contiene immagini o altri file su superconduttività
  

Collegamenti esterni |

• 
  


• 
  Superconduttività, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
  


• 
  (EN) Superconduttività, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
  


• R. W. Dull e H. R. Kerchner, A teacher's guide to superconductivity for high school students (PDF), Oak Ridge National Laboratory, 1994, DOI:10.2172/10196269. URL consultato il 21 ottobre 2008.


• 
  Carlo Di Castro and Roberto Raimondi, An introduction to superconductivity, part I (PDF), in Proceedings of the XXIV Italian National School of Condensed Matter Physics, Bra, (Italy), S. Pace and M.Acquarone, settembre 1989. URL consultato il 21 ottobre 2008.
  
  • An introduction to superconductivity, part II (PDF). URL consultato il 21 ottobre 2008.
  
  


• Introduction to Superconductivity: Fundamentals and Applications, Boulder, Stati Uniti,, Scuola di fisica della materia condensata, 2000. URL consultato il 21 ottobre 2008 (archiviato dall'url originale il 6 novembre 2008).


• (EN) Dissemination of IT for the Promotion of Materials Science (DoITPoMS), "Superconductivity", su doitpoms.ac.uk.


• [2]

Portale Fisica

Portale Materiali