Rifrazione atmosferica
Fotografia della Luna piena parzialmente offuscata dall'atmosfera terrestre. Da notare che la forma del bordo inferiore della Luna non è circolare a causa della rifrazione.
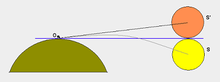
Il diagramma mostra lo spostamento dell'immagine del Sole all'alba e al tramonto.
La rifrazione atmosferica è la deviazione della luce, o di altra onda elettromagnetica, da una linea retta mentre passa attraverso l'atmosfera dovuta al variare della densità dell'aria in base all'altezza. La rifrazione atmosferica può far sì che oggetti distanti appaiano brillare o incresparsi, più in alto o più in basso, più allungati o più accorciati. Inoltre, vicino al suolo può causare miraggi. Il termine si applica anche alla rifrazione del suono.
La rifrazione atmosferica fa apparire gli oggetti celesti nel cielo più alti di quanto non lo siano nella realtà. Agisce non solo sui raggi della luce, ma su tutte le radiazioni elettromagnetiche, anche se con diverso grado (vedi dispersione ottica). Ad esempio, nella luce visibile, il blu subisce maggior rifrazione del rosso. Ciò può essere causa, nelle immagini ad alta risoluzione di oggetti astronomici, di dispersione in uno spettro.
Quando possibile, gli astronomi programmano le loro osservazioni intorno al momento di culminazione di un oggetto, vale a dire quando è più alto nel cielo. Ugualmente i marinai non osserverebbero una stella di altezza inferiore a 20°. Se le osservazioni vicino all'orizzonte non possono essere evitate, è possibile dotare un telescopio di sistemi di controllo per compensare lo spostamento causato dalla rifrazione. Se c'è anche un problema di dispersione (in caso di osservazioni in banda larga ad alta risoluzione), può essere impiegato anche un correttore di rifrazione atmosferica (costituito da coppie di prismi di vetro rotanti). Ma quando l'entità della rifrazione atmosferica dipende dalla temperatura e dalla pressione, nonché dall'umidità (la quantità di vapore acqueo è particolarmente importante a lunghezze d'onda infrarosse medie), lo sforzo necessario per un'adeguata compensazione potrebbe essere proibitivo.
La rifrazione atmosferica diventa più intensa quando non è omogenea, quando c'è turbolenza nell'aria per esempio. Questa è la causa dello scintillio delle stelle e della deformazione del sole all'alba e al tramonto.
Indice
1 Valori
2 Calcolo rifrazione
3 Turbolenze nell'atmosfera
4 Note
5 Voci correlate
6 Altri progetti
7 Collegamenti esterni
Valori |
La rifrazione atmosferica è pari a zero allo zenit, meno di 1' (un minuto d'arco) a 45° di altezza apparente, e solo 5,3' a 10°, ma aumenta rapidamente col diminuire dell'altezza, raggiungendo i 9,9' a 5°, 18,4 'a 2°, e il 35,4' all'orizzonte;[1] tutti i valori sono per 10 °C e 101,3 kPa.
All'orizzonte, la rifrazione è leggermente maggiore del diametro apparente del Sole. Perciò, quando sembra che il disco completo del sole sia appena sopra l'orizzonte, nessuna parte del disco del sole sarebbe visibile se non fosse per l'atmosfera. Per convenzione, l'alba e il tramonto si riferiscono al momento in cui il limbo superiore del Sole appare o scompare rispetto all'orizzonte. Il valore standard per l'altezza vera del Sole è -50': -34' per la rifrazione e -16' per il semidiametro del Sole (l'altezza di un corpo celeste viene data di norma per il centro del disco). Nel caso della Luna, ulteriori correzioni sono necessarie per la parallasse orizzontale della stessa e per il suo semidiametro apparente; entrambi variano con la distanza Terra-Luna.
Le variazioni giornaliere del tempo atmosferico hanno influenza sui momenti esatti dell'alba e del tramonto,[2] nonché sul sorgere e sul tramonto della Luna, ed è questo il motivo per cui in genere non è ritenuto significativo dare i tempi dell'alba e del tramonto con una precisione maggiore dell'arrotondamento al minuto.[3]
Calcoli più precisi possono essere utili per determinare i tempi di alba e tramonto con il valore standard di rifrazione[4], tenendo conto che i tempi effettivi potrebbero essere diversi a causa di variazioni non prevedibili della rifrazione.
Poiché la rifrazione atmosferica è di 34' all'orizzonte, ma solo 29' a 0,5° sopra di esso, il Sole del tramonto o dell'alba sembra essere appiattito di circa 5' (1/6 circa del suo diametro apparente).
Calcolo rifrazione |
Il calcolo rigoroso della rifrazione richiede l'integrazione numerica, con l'utilizzo di un metodo come quello di Auer e Standish.[5] Bennett[6] ha sviluppato una formula empirica semplice per calcolare la rifrazione partendo dall'altezza apparente. Usando l'algoritmo di Garfinkel[7] come riferimento, se ha è l'altezza apparente in gradi, la rifrazione R in minuti d'arco è data da
- R=cot(ha+7.31ha+4.4);{displaystyle R=cot left(h_{mathrm {a} }+{frac {7.31}{h_{mathrm {a} }+4.4}}right),;}
la formula ha una precisione di 0,07'.[3]
Saemundsson[8] ha sviluppato una formula per determinare la rifrazione partendo dall'altezza vera; se h è l'altezza vera in gradi, la rifrazione R in minuti d'arco è data da
- R=1.02cot(h+10.3h+5.11);{displaystyle R=1.02cot left(h+{frac {10.3}{h+5.11}}right),;}
la formula corrisponde a quella di Bennett a meno di 0,1'. Entrambe le formule assumono una pressione atmosferica di 101 kPa ed una temperatura di 10 °C. Per differenti pressioni P e temperature T, la rifrazione calcolata con queste formule va moltiplicata per
P1010283273+T{displaystyle {frac {P}{1010}},{frac {283}{273+T}}}[3] La rifrazione aumenta dell'1% circa per ogni aumento di 0,9 kPa della pressione, e diminuisce dell'1% circa per ogni diminuzione di 0,9 kPa della pressione. Allo stesso modo, la rifrazione aumenta dell'1% circa per ogni 3 °C di diminuzione della temperatura, e diminuisce dell'1% circa per ogni aumento di 3 °C di temperatura.
Turbolenze nell'atmosfera |
Le turbolenze nell'atmosfera ingrandiscono o rimpiccioliscono le immagini delle stelle, facendole apparire più luminose o più deboli su una scala di tempo di millisecondi. Le componenti più lente di queste fluttuazioni sono visibili agli occhi sotto forma di scintillio.
Le turbolenze provocano anche piccoli movimenti casuali dell'immagine della stella, e producono rapidi cambiamenti nella sua struttura. Questi effetti non sono visibili ad occhio nudo, ma lo diventano nei telescopi anche se piccoli. Gli astronomi li chiamano "seeing".
Note |
^ Allen, C. W. 1976. Astrophysical Quantities, 3rd ed. 1973, reprinted with corrections, 1976. London: Athlone. ISBN 0-485-11150-0
^ Schaefer, Bradley E., and William Liller. 1990. Refraction near the horizon. Publications of the Astronomical Society of the Pacific 102: 796–805, July 1990.
^ abc Meeus, Jean. 1991. Astronomical Algorithms. Richmond, Virginia: Willmann-Bell, Inc. ISBN 0-943396-35-2
^ Meeus, Jean. 2002. More Mathematical Astronomy Morsels. Richmond, Virginia: Willmann-Bell, Inc. ISBN 0-943396-74-3
^ Auer, Lawrence H., and E. Myles Standish. 2000. Astronomical Refraction: Computation for All Zenith Angles. Astronomical Journal 119, no. 5 (May):2472–2474.
^ Bennett, G.G. 1982. The Calculation of Astronomical Refraction in Marine Navigation. Journal of Navigation 35:255–259. DOI (payment required)
^ Garfinkel, B. 1967. Astronomical Refraction in a Polytropic Atmosphere. Astronomical Journal 72:235–254.
^ Sæmundsson, Þorsteinn. 1986. Astronomical Refraction. Sky and Telescope 72 (July):70.
Voci correlate |
- Rifrazione
- Alhazen
Altri progetti |
Altri progetti
- Wikimedia Commons
Wikimedia Commons contiene immagini o altri file su Rifrazione atmosferica
Collegamenti esterni |
Rifrazione atmosferica, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
Astronomical Refraction—Andrew T. Young- Java Programming1, su geocities.jp.
- Java Programming2, su geocities.jp.
- JavaScript calculator, su geocities.jp.
