Meridiana

Multi tool use
.mw-parser-output .nota-disambigua{clear:both;margin-bottom:.5em;border:1px solid #CCC;padding-left:4px}.mw-parser-output .nota-disambigua i{vertical-align:middle}

Orologio solare a Colla Micheri.
La meridiana, detta anche, impropriamente, orologio solare o quadrante solare, è uno strumento di misurazione del tempo basato sul rilevamento della posizione del Sole.[1] Ha origini molto antiche e nella sua accezione più generale indica in massima parte gli orologi solari presenti sui muri degli edifici. In senso stretto, con meridiana si deve intendere unicamente l'indicatore del passaggio del Sole a mezzogiorno.
Il termine "quadrante solare", che caratterizza 'non' le meridiane bensì gli orologi solari, trae la sua origine dal latino quadrans che indicava nel Rinascimento la quarta parte di cerchio sulla quale veniva generalmente tracciato un orologio solare portatile, denominato appunto quadrante. Tuttavia, il suo significato è stato generalizzato nel linguaggio popolare, in tempi moderni, divenendo sinonimo di meridiana[1] e orologio solare.[2]
A differenza dell'orologio solare,la meridiana indica ogni giorno, lungo una linea retta, l'istante in cui il Sole transita sul meridiano del luogo alle ore 12.
Indice
1 Introduzione
2 Orologio solare fisso
2.1 Equatoriali o equinoziali
2.2 Orologi solari orizzontali da giardino
2.3 Verticali o murali
2.4 Orologio negativo solare
3 Orologi solari portatili
3.1 A dittico
3.2 Ad elevazione
3.3 Telescopica
4 Meridiana a tempo medio
4.1 Orologio solare equatoriale a coppa
4.2 Orologio solare greco
4.3 Le vere Meridiane: orologi del mezzodì
4.4 A riflessione
4.5 Meridiana calcolatrice
5 Meridiane digitali
6 Meridiane naturali
6.1 Galleria d'immagini
7 Note
8 Bibliografia
9 Voci correlate
10 Altri progetti
11 Collegamenti esterni
Introduzione |

Un orologio solare (in Piazza del Collegio Ghislieri a Pavia)
Gli orologi solari e le meridiane erano già conosciuti nell'antico Egitto e presso altre civiltà, e successivamente tra quella dei Greci e dei Romani.
L'origine di questa scienza è tuttavia ancor più antica rispetto alla civiltà egizia e le prime testimonianze risalgono addirittura al Neolitico.
Lo studio degli orologi solari è chiamato gnomonica o, meno frequentemente, sciaterica.
Nella forma tradizionale l'orologio solare è uno stilo, detto gnomone, che proietta la sua ombra su una superficie orizzontale o verticale, detta quadrante, indicando l'ora solare locale.
Mentre nella meridiana il Mezzogiorno locale è indicato sopra una linea retta, nell'orologio solare l'ora locale è definita in modo più esteso sopra un quadrante nel quale, l'angolo orario di tutte le ore è un multiplo di 15°. Questo orario differisce dall'orario dell'orologio che portiamo al polso perché quest'ultimo indica l'ora media in vigore nei vari paesi.
I due orari sono differenti per altri motivi:
- Equazione del tempo
- Il giorno solare, ovvero l'intervallo tra due transiti del Sole su uno stesso meridiano, dura in media ventiquattro ore. A causa della differente velocità di rivoluzione della Terra attorno al Sole e dell'obliquità dell'eclittica, la durata del giorno non è costante, cioè il giorno vero non dura mai ventiquattro ore come il giorno medio, ma è un po' più lungo o un po' più corto. Le differenze, sommandosi tra loro, generano un divario tra il tempo vero e il tempo medio che arriva a ±15/16 minuti, determinando la cosiddetta Equazione del tempo (Edt), così definita:
- Edt = Tempo solare medio - Tempo solare vero (o viceversa).
- Longitudine della località
- L'ora media di ogni paese ha uno o più meridiani di riferimento. In Italia il meridiano di riferimento è quello di longitudine 15° Est rispetto a Greenwich. La differenza tra il transito del Sole sul meridiano centrale e quello del meridiano locale di longitudine L ha un valore costante di (15°-L)*4 minuti. Per confrontare un quadrante a ora vera locale con l'orologio, questa differenza va integrata con l'equazione del tempo.
Ad esempio, in un luogo avente longitudine 12° Est, nel 2015 la differenza massima tra l'orologio da polso e un quadrante a ora vera locale si verifica l'11 febbraio quando l'equazione del tempo, pari a 14m 11.5s, si somma alla differenza dovuta alla longitudine pari a: (15°-12°)*4min=12min, comportando uno scarto di 26m 11.5s.
In alcuni casi le linee orarie della meridiana, anziché indicare l'ora vera locale, indicano l'ora vera del fuso di riferimento. In questi quadranti, quando l'ombra segna le 12, il Sole transita sul meridiano centrale. Pertanto per confrontare l'ora indicata da queste meridiane con quella di un orologio da polso è sufficiente apportare solo la correzione dell'equazione del tempo.
Una meridiana verticale a ora vera locale si riconosce rispetto a una a ora vera del fuso osservando la linea del mezzogiorno, perfettamente verticale nel primo caso, leggermente ruotata nel secondo.
Su molti orologi solari, le differenze tra l'ora del quadrante e quella media dell'orologio da polso sono riprodotte in una tabella, oppure sono sintetizzati in un grafico. In alcuni casi nel quadrante è tracciato l'analemma (o lemniscata), ossia la curva a forma di 'otto' che indica l'ora media del fuso e permette di leggere direttamente l'ora dell'orologio senza ricorrere alla correzione dell'equazione del tempo e della differenza di longitudine.
Lo gnomone di un quadrante può essere di diversi tipi, per esempio: ortostilo, stilo polare, a camera oscura, bifilare, a riflessione.
Nei quadranti verticali gli gnomoni più usati sono l'ortostilo e lo stilo polare. L'ortostilo è piantato ortogonale alla parete e indica l'ora con la punta dello gnomone. Lo stilo polare è invece posizionato in modo da risultare parallelo all'asse di rotazione terrestre, quindi punta il polo celeste e la sua ombra coincide con la linea oraria in tutta la sua lunghezza.
Orologio solare fisso |
Equatoriali o equinoziali |
La più semplice forma di orologio solare è costituita da un disco coassiale con una barra collocata parallelamente all'asse terrestre. Il disco forma un piano parallelo con l'equatore. Sul disco sono tracciati dei segni che indicano il trascorrere delle ore. Normalmente il mezzogiorno è collocato nella parte più bassa del disco, le 6 al bordo ovest e le 18 al bordo est. In estate la parte nord del disco è illuminata mentre la parte sud non lo è. In inverno è illuminata la parte sud e non la nord. In estate il nodo è l'estremità a nord dello gnomone, in inverno lo diventa l'estremità sul lato opposto del disco.
Sul disco possono essere tracciati una serie di cerchi concentrici per evidenziare la posizione del nodo ogni giorno, permettendo di usare l'orologio come calendario.
Uno svantaggio di questa soluzione è che agli equinozi i raggi solari giungono parallelamente al disco e lo strumento è difficilmente leggibile.
Orologi solari orizzontali da giardino |

Orologio solare orizzontale
L'orologio solare da giardino si basa sullo stesso principio della precedente, ma le linee del disco sono proiettate per mezzo della trigonometria su un piano parallelo al suolo. Il principale vantaggio di questo sistema è di potere mostrare l'ora tutto l'anno, poiché il quadrante non è mai completamente in ombra. I numeri sono in senso antiorario nell'emisfero settentrionale e in senso orario nell'emisfero meridionale. Il quadrante può essere tracciato sulla pavimentazione di una piazza oppure su un disco di vetro traslucido visibile dal basso.
Dalla base dello gnomone verso il bordo del quadrante sono tracciate le linee corrispondenti alle ore. Gli angoli di queste linee sono calcolati con la formula:
- angolo=arctan(sin(latitudine)⋅tan(angolo orario)){displaystyle {mbox{angolo}}=arctan(sin({mbox{latitudine}})cdot tan({mbox{angolo orario}}))}
L'inclinazione dello gnomone rispetto al quadrante è pari alla misura in gradi della latitudine del posto in cui ci troviamo. Lo strumento ovviamente deve essere orientato, cioè occorre ruotare il quadrante in modo che lo gnomone sia parallelo all'asse terrestre.
Verticali o murali |
Sebbene oggigiorno siano una rarità, un tempo gli orologi solari tracciati sulle pareti esterne degli edifici esposte a sud erano comuni (o quadrante rivolto a nord nell'emisfero sud), poiché visibili a distanza ed economici da realizzare. Il quadrante era semplicemente dipinto sul muro oppure ricavato su una lastra di marmo o pietra. Lo gnomone era uno stilo di ferro o di ottone, oppure un tripode di metallo, per maggiore robustezza.
Principale svantaggio di questi strumenti è che sono in grado di mostrare l'ora solamente per il periodo dell'anno e del giorno in cui il muro è direttamente illuminato dal sole.
La progettazione è molto simile a quella dei modelli orizzontali; la formula per un quadrante esposto a sud è:
- angolo=arctan(cos(latitudine)⋅tan(angolo orario)){displaystyle {mbox{angolo}}=arctan(cos({mbox{latitudine}})cdot tan({mbox{angolo orario}}))}
L'inclinazione dello gnomone è uguale alla latitudine.
Tradizionalmente si usava collocare quattro orologi sul tetto o sulle pareti perimetrali di una torre, in modo da avere l'indicazione per tutto l'anno. È abitudine incidere sul quadrante un motto.

Orologio solare a muro
Issoire, Alvernia, Francia - Orologio Solare sulla porta est della città

"Finta meridiana" dipinta sul muro di una villa sulla via Aurelia presso San Bartolomeo al Mare, Imperia
Aldeburgh, Suffolk, England

Chiesa dei ss. Nicolò ed Erasmo, Voltri
Antico orologio solare del 1699, a San Benigno Canavese

Meridiana al Castello di Buona Speranza, Città del Capo (Nota - emisfero australe).
Orologio negativo solare |
Negli orologi solari convenzionali lo gnomone proietta l'ombra su un quadro di riferimento, l'orologio negativo è quello che proietta i raggi di luce attraverso una fessura.

Orologio negativo solare, Corregidora, Querétaro, Messico
Orologi solari portatili |
.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}
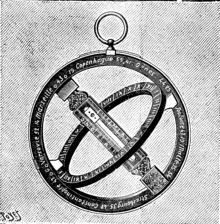
Un orologio solare portatile ad elevazione costruito a Parigi da Butterfield, probabilmente alla fine del XVIII secolo
A partire dal Medioevo furono elaborati strumenti astronomici e orologi solari portatili.
A dittico |
Un tipo molto comune è costituito da due piccoli pannelli (un dittico) di legno o meglio avorio bianco intarsiato, incernierati in modo da potere essere chiudibili a formare una scatola facilmente trasportabile.
Lo gnomone è realizzato con un filo di lino, seta o canapa teso tra le due tavole.
Quando il filo è teso, le due tavole costituiscono due quadranti, uno orizzontale e uno verticale.
Un errore comune è descrivere questo strumento come auto allineante. Ciò non è corretto per gli orologi solari a dittico che utilizzano un filo tra le due tavole, indipendentemente dall'orientamento dei quadranti. Dato che il filo è continuo, le ombre devono incontrarsi sulla cerniera; perciò, qualunque orientamento dello strumento mostrerà la stessa ora sui due quadranti.
A mezzogiorno, al tramonto e all'alba, la variazione di latitudine non influisce sull'ora mostrata dall'orologio solare portatile, ma alle 9 e alle 15 ogni grado di errore nella latitudine produce una differenza di quattro minuti nell'ora mostrata sui due quadranti. Ne consegue che può essere usato come un astrolabio o un sestante per determinare la latitudine.
Alcuni strumenti comprendono una scala con un filo a piombo su cui leggere la latitudine, mentre altre includono una rosa dei venti. Orologi solari di questo tipo di grandi dimensioni (oltre il metro) erano usati per la navigazione.
Ad elevazione |
La funzione dell'orologio solare poteva essere svolta da un astrolabio, usato anche per la navigazione e l'astronomia. Nel modello più semplice era costituito da un anello sostenuto da un anellino. Quando il tutto era tenuto in mano in modo che penzolasse verticalmente, un foro nell'anello (detto foro gnomonico) proiettava un punto luminoso all'interno, dove una scala indicava l'ora. lo strumento era vincolato ad una particolare latitudine e l'utilizzatore doveva sapere a priori se era mattino o pomeriggio, altrimenti indistinguibili. Il foro era montato su di una slitta regolabile in funzione del giorno dell'anno.
In tempi moderni le forze speciali dell'esercito degli Stati Uniti dispongono di un semplice orologio solare di questo tipo ricavata nel coltello in dotazione all'equipaggiamento, utile in caso di malfunzionamento dell'orologio meccanico.
Telescopica |
William Molyneux inventò nel 1686 una "meridiana telescopica" (in latino sciothericum telescopicum) che faceva uso di un telescopio per determinare il mezzogiorno esatto, a beneficio della precisione in navigazione, astronomia e geografia.[3]
Meridiana a tempo medio |

Orologio solare di precisione a Bütgenbach, Belgio. (precisione = ±30 secondi) (Google Earth)
Una meridiana può essere anche chiamata eliocronometro, perché è in grado di correggere il tempo solare apparente per indicare il tempo solare medio o un altro tempo standard, solitamente con un'accuratezza nell'ordine del minuto.
Orologio solare equatoriale a coppa |
La più classica forma di eliocronometro è quello con quadrante a coppa, sopra il quale una barra e filo teso parallelamente all'asse terrestre costituisce lo gnomone. La scala è tracciata a formare un semicerchio all'interno della coppa.
Questo tipo di strumento fu usato in Francia durante la prima guerra mondiale per regolare l'orario dei treni.
Gli strumenti più precisi si trovano a Jaipur in India. Sono di dimensioni colossali e furono fatte costruite dal califfo Mogul per tenere aggiornato il calendario islamico.
Orologio solare greco |

Orologio solare di Cnido
Gli antichi Greci usarono un tipo di orologio solare chiamato "pellekinos".[4] Lo gnomone era una barra o un palo messo verticalmente su un piano orizzontale o semisferico. L'ombra della punta dello gnomone descriveva una curva iperbolica sulla superficie piatta o circolare sulla superficie semisferica. Sulla superficie erano tracciate linee che indicavano l'ora esatta in ogni periodo dell'anno.
Le vere Meridiane: orologi del mezzodì |

Meridiana del mezzodì a tempo medio (Chiesa riformata di Santa Maddalena ad Avenches (Canton Vaud Svizzera)
Questo tipo di meridiana è caratterizzato dall'avere la linea delle ore a forma di 8 (detta analemma), corrispondente alla rappresentazione visiva dell'equazione del tempo. L'ora è letta nel punto in cui l'ombra del nodo dello gnomone cade sulla curva analemmatica. Questo compensa automaticamente gli effetti combinati dell'eccentricità dell'orbita terrestre e dell'inclinazione dell'asse di rotazione. Segnano il "Tempo Medio".
A riflessione |
Isaac Newton inventò una meridiana adatta per le finestre esposte a sud. Egli collocò un piccolo specchio sul davanzale della finestra e dipinse un quadrante simile al pelekînos greco sul soffitto e sulle pareti. Lo specchio costituisce in questo caso lo gnomone riflettendo il punto luminoso. In questo modo è possibile realizzare uno strumento ampio, accurato e facilmente correggibile con poco materiale e senza spreco di spazio. Il quadrante può anche essere di tipo analemmatico.
Meridiana calcolatrice |
Una interessante variante della meridiana orizzontale è in grado di elaborare e mostrare direttamente il tempo standard.
Diversamente da un modello normale, sul quadrante gli intervalli orari sono tracciati con angoli identici.
Ad esso è sovrapposta una maschera a forma di cardioide (una figura geometrica a forma di cuore).
Questa figura esprime la formula di corrispondenza tra i differenti angoli orari di una meridiana convenzionale e gli angoli orari identici come appaiono sul quadrante di un orologio.
Il punto in cui l'ombra dello gnomone incontra la curva cardioide è dove si deve leggere l'ora sul quadrante sottostante. La correzione dell'ora legale viene effettuata semplicemente ruotando il quadrante inferiore.
Meridiane digitali |
Una meridiana digitale sfrutta le luci e le ombre per mostrare l'ora sotto forma di cifre o anche parole, invece del tradizionale sistema basato sulla posizione. Un sistema è quello di affacciare due maschere parallele con coppie di fori che risultano allineate e consentono il passaggio dei raggi luminosi ciascuna in preciso periodo del giorno.
Meridiane naturali |
Una meridiana naturale sfrutta la conformazione del suolo per mostrare l'ora grazie alle cime montuose che il sole illumina. Un esempio di tale regalo della natura è la meridiana di Sesto, che con le sue cime dolomitiche fornisce questo strumento.
Galleria d'immagini |

Alatri, orologio solare a tempo vero e medio di Angelo Secchi
Alessandria, orologio solare murale (solo decorativo) in via Caraglio
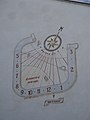
Un interessante e insolito orologio solare indicante l'ora solare e quella legale ad Alessandria, via Giovanni Aliora
Orologio solare a Bergamo, sfera armillare semplificata tempo vero e medio anno 2002 Mauro Fizzanotti

La meridiana catottrica di Brescia[5]

Orologio solare su una casa di Cervo
Orologio solare a Cracovia
Leri Cavour, orologio solare, 1856

Meridiana solare nel Duomo di San Giorgio a Modica
"Orologio del Dodecaedro" a Palermo, dove per ogni faccia si trova un orologio solare, progettato dal matematico Lorenzo Federici

Orologio solare sulla facciata sud della ex Caserma Damiano Chiesa a Rovereto. Immagine ripresa da via Santa Maria, sul Ponte Forbato. Leggibile la scritta: noi siamo in tre. Occhio, sole e me.
Tortona, meridiana in piazza Obizzo Malaspina

Meridiana bifilare in acciaio inox a Trento
Note |
^ ab Meridiana, in Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana, 15 marzo 2011. URL consultato il 31 luglio 2016.
^ Glossario, su artesolare.it.
^ (EN) William Molyneux, Sciothericum telescopicum, or A new contrivance of adapting a telescope to an horizontal dial for observing the moment of time by day or night, 1686.
^ Vitruvio 9.8.1
^ Meridiana catottrica di Brescia
Bibliografia |
- Piero Bianconi e Aldo Morosoli, Meridiane del Ticino, Unione Svizzera delle Casse Raiffeisen, San Gallo
- René R. J. Rohr, Meridiane. Storia, teoria, pratica, Ulisse, Torino 1988 ISBN 88-414-3013-3
Renzo Morchio, Scienza e poesia delle meridiane, ECIG, Genova 1988 ISBN 88-7545-253-9
- Giovanni Bosca e Piero Stroppa, Meridiane e orologi solari, Trezzano sul Naviglio, Il Castello, 1996 ISBN 88-8039-022-8
- Giovanni Paltrinieri, Meridiane e orologi solari d'Italia, L'Artiere, Bentivoglio (Bologna), 1997
- Giancarlo Pavanello e Aldo Trinchero, Le meridiane, De Vecchi, Milano 1999 ISBN 88-412-4691-X
Giordano Berti e Giovanni Paltrinieri (a cura di), Gian Domenico Cassini. La Meridiana del Tempio di S. Petronio in Bologna, Arnaldo Forni Editore, S. Giovanni in Persiceto, 2000.
Giordano Berti e Giovanni Paltrinieri (a cura di), Luoghi del tempo nella provincia di Bologna. Meridiane, orologi solari e orologi meccanici, Istituto Graf, Bologna 2008. La mappa è visibile anche sul Portale Turismo della Provincia di Bologna [1]
- Nicola Severino: Storia della Gnomonica, Roccasecca, 1992-1994, Antologia di Storia della Gnomonica, 1995, Storia dell'Astrolabio, 1995, La gnomonica kircheriana e le Tavole Sciateriche di Monte Porzio Catone, 1995, Gnomonica Cinese, 1996, International Bibliography of Gnomonica, 1997, Gnomonica, la prima rivista italiana sugli orologi solari, Orologi solari Greco-Romani, 2003, De Monumentis Gnomonicis apud Graecos et Romanos, 2005. Web, http://www.nicolaseverino.it
- Nicola Ulivieri, I segreti degli orologi solari, Youcanprint 2015 ISBN 978-88-9114-852-0
- Carlo Burin, L'orologio solare moderno a quadrante piano, come funziona come si calcola, Aracne editrice S.r.l., Roma 2010 ISBN 978-88-548-3526-9
Voci correlate |
- Gnomonica
- Meridiana (indicatore)
- Meridiana a cannone
- Sciaterica
- Tavole sciateriche
- Grande meridiana di Bari
Altri progetti |
Altri progetti
- Wikiquote
- Wikizionario
- Wikimedia Commons
 Wikiquote contiene citazioni sulla meridiana
Wikiquote contiene citazioni sulla meridiana
 Wikizionario contiene il lemma di dizionario «meridiana»
Wikizionario contiene il lemma di dizionario «meridiana»
 Wikimedia Commons contiene immagini o altri file sulla meridiana
Wikimedia Commons contiene immagini o altri file sulla meridiana
Collegamenti esterni |
.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}
.mw-parser-output .CdA{border:1px solid #aaa;width:100%;margin:auto;font-size:90%;padding:2px}.mw-parser-output .CdA th{background-color:#ddddff;font-weight:bold;width:20%}
| Controllo di autorità | GND (DE) 4055589-6 · BNF (FR) cb11931091v (data) |
|---|
kv hQRWB7n6R























