CMOS

Multi tool use
Questa voce o sezione sugli argomenti componenti per computer e elettronica non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Nessuna fonte |
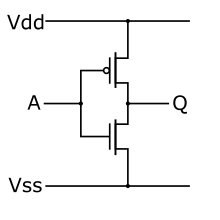
Circuito semplificato dell'invertitore a tecnologia CMOS
Il CMOS (acronimo di complementary metal-oxide semiconductor) è un tipo di tecnologia utilizzata in elettronica digitale per la progettazione di circuiti integrati, alla cui base sta l'uso dell'invertitore a transistor MOSFET.
Indice
1 Descrizione
1.1 Caratteristiche
1.2 Elementi base
1.3 FSI e BSI
2 Potenza dinamica dissipata
2.1 Potenza di cortocircuito
2.2 Potenza associata alla carica/scarica del condensatore
3 Note
4 Voci correlate
5 Altri progetti
6 Collegamenti esterni
Descrizione |
Si tratta di una struttura circuitale costituita dalla serie di una rete di "Pull-Up" ed una di "Pull-Down": la prima s'incarica di replicare correttamente il livello logico alto LL1 mentre alla seconda è destinata la gestione del livello logico basso LL0. Tale topologia circuitale fu inventata da Frank Wanlass nel 1967.
La rete di Pull-Up è costituita da MOSFET a canale P, che si "accendono" solo se la tensione presente sul gate (misurata rispetto al source) è minore della tensione di soglia. Inversamente la rete di Pull-Down è costituita da MOSFET a canale N che si accendono solo se la tensione presente sul gate (misurata rispetto al source) è maggiore della tensione di soglia.
Per comprendere come sia strutturata la tecnologia CMOS può risultare utile osservare una porta logica NOT realizzata con tecnologia CMOS. Si può notare come, nell'eventualità che il segnale d'ingresso sia a LL1, sia il solo N-MOS ad attivarsi portando l'uscita a LL0. Inversamente, con l'ingresso a LL0, è il solo P-MOS ad attivarsi portando l'uscita a LL1. Particolarità di questa porta logica è di avere una dinamica logica d'uscita piena, cioè pari alla massima tensione applicata, Vcc; inoltre né la rete di pull-up né la rete di pull-down soffre di effetto body. La componentistica realizzata in questa tecnologia è caratterizzata da un consumo di corrente estremamente basso.
Caratteristiche |

Sezione trasversale di due transistor in una porta CMOS

Processo semplificato di microfabbricazione.
NB: i contatti di gate, source e drain non sono realmente sullo stesso piano, e il diagramma non è in scala.
Uno dei principali vantaggi della logica CMOS è di avere una potenza statica dissipata idealmente nulla: questa caratteristica è dovuta alla complementarità del pull-down (n-Mos) e del pull-up (p-Mos); ossia, quando è acceso il pull-up, è spento il pull-down, e viceversa.
In realtà ci sono piccole correnti di perdita (per caricare/scaricare le capacità parassite, la corrente di cortocircuito durante la commutazione di stato, per perdite alle giunzioni e per le correnti di sottosoglia), trascurabili se il numero dei MOS è relativamente piccolo, ma che può diventare particolarmente sentito, in particolare le correnti di sottosoglia sono responsabili di circa la metà della dissipazione di potenza nelle attuali realizzazioni VLSI.
Elementi base |
Dimensionando opportunamente i due MOS (simmetrici dal punto di vista funzionale) è possibile avere una curva caratteristica simmetrica, soluzione ottima per avere il margine di immunità ai disturbi il più elevato possibile. Il tratto di caratteristica ad alto guadagno è indipendente dal rapporto tra i fattori di forma dei due MOS (ratioless).
Gli elementi base per costruire qualsiasi circuito digitale sono:
NAND: realizzato con pull-up costituito da due p-Mos in parallelo e pull-down da due n-Mos in serie
NOR: realizzato con pull-up costituito da due p-Mos in serie e pull-down da due n-Mos in parallelo
Ogni funzione logica binaria può essere espressa in termini di questi due operatori.
FSI e BSI |
Originariamente i CMOS hanno una struttura del tipo FSI (front side illumination), dove lo strato di silicio (fotosensori) è posto in fondo, mentre con la disposizione BSI (backside illumination) dato che lo strato di silicio è posto sopra gli strati metallici (servono al fotodiodo per convertire i fotoni della luce in elettroni, quindi in segnali elettrici), il che permette una maggiore sensibilità alla luce e per via della disposizione anche una maggiore fedeltà al colore (minori contaminazioni dei pixel adiacenti) e possibilità di adoperare ottiche più compatte.[1]
Potenza dinamica dissipata |
Si possono identificare due tipi di dissipazioni di potenza dinamica:
- Potenza di cortocircuito
- Potenza associata alla carica/scarica del condensatore
- ⟨P⟩=1T∫P(t)dt{displaystyle langle Prangle ={frac {1}{T}}int P(t)operatorname {d} t}
Potenza di cortocircuito |
Trascurando la capacità parassita Cl{displaystyle C_{l}}


Dall'istante ta{displaystyle t_{a}}



Quindi la potenza avrà un valore non nullo in quei punti; ricordiamo che la potenza dinamica è:

Grafico della Vi{displaystyle V_{i}}
 e Id{displaystyle I_{d}}
e Id{displaystyle I_{d}} rispetto al tempo della logica CMOS
rispetto al tempo della logica CMOS- Pd=Vdd∗Id {displaystyle P_{d}=V_{dd}*I_{d} }
Quindi calcoliamo la potenza attiva:
- ⟨Pd⟩=1T[∫tatbPddt+∫tbtcPddt+∫tdtePddt+∫tetfPddt]={displaystyle langle P_{d}rangle ={frac {1}{T}}left[int _{t_{a}}^{t_{b}}P_{d}operatorname {d} t+int _{t_{b}}^{t_{c}}P_{d}operatorname {d} t+int _{t_{d}}^{t_{e}}P_{d}operatorname {d} t+int _{t_{e}}^{t_{f}}P_{d}operatorname {d} tright]=}
- =VddT[∫tatbIdn,sat(t)dt+∫tbtcIdp,sat(t)dt+∫tdteIdp,sat(t)dt+∫tetfIdn,sat(t)dt]{displaystyle ={frac {V_{dd}}{T}}left[int _{t_{a}}^{t_{b}}I_{dn,sat}(t)operatorname {d} t+int _{t_{b}}^{t_{c}}I_{dp,sat}(t)operatorname {d} t+int _{t_{d}}^{t_{e}}I_{dp,sat}(t)operatorname {d} t+int _{t_{e}}^{t_{f}}I_{dn,sat}(t)operatorname {d} tright]}
Facendo l'ipotesi di MOS complementari
- βn=βp {displaystyle beta _{n}=beta _{p} }
- Vtn=|Vtp|=Vt {displaystyle V_{tn}=|V_{tp}|=V_{t} }
Allora
- Idn,sat=Idp,sat {displaystyle I_{dn,sat}=I_{dp,sat} }
Si viene ad avere
- ⟨Pd⟩=4VddT[∫tatbβn2(Vgsn(t)−Vtn)2dt]{displaystyle langle P_{d}rangle ={frac {4V_{dd}}{T}}left[int _{t_{a}}^{t_{b}}{frac {beta _{n}}{2}}(V_{gsn}(t)-V_{tn})^{2}operatorname {d} tright]}
Possiamo conoscere gli estremi di integrazione tramite l'equazione
- t:tr=Vi(t):Vdd {displaystyle t:t_{r}=V_{i}(t):V_{dd} }
- t=tr∗Vi(t)Vdd {displaystyle t=t_{r}*{frac {V_{i}(t)}{V_{dd}}} }
- Vi(t)=Vgsn(t) {displaystyle V_{i}(t)=V_{gsn}(t) }
Sostituendo e risolvendo si ha:
- ⟨Pd⟩=β∗tr∗Vdd312T[1−2VtnVdd]{displaystyle langle P_{d}rangle =beta *t_{r}*{frac {V_{dd}^{3}}{12T}}left[1-{frac {2V_{tn}}{V_{dd}}}right]}

Grafico della Vo{displaystyle V_{o}}
 e Id{displaystyle I_{d}}
e Id{displaystyle I_{d}} rispetto a Vi{displaystyle V_{i}}
rispetto a Vi{displaystyle V_{i}} della logica CMOS
della logica CMOSFacendo l'ipotesi Vdd>>Vtn{displaystyle V_{dd}>>V_{tn}}
- ⟨Pd⟩=β∗tr∗Vdd312T{displaystyle langle P_{d}rangle =beta *t_{r}*{frac {V_{dd}^{3}}{12T}}}
Nota: Dipende:
- linearmente dalla durata del fronte di salita (o di discesa)
- dal cubo della tensione di alimentazione
- inversamente dal Periodo (cioè, aumentando la frequenza di lavoro, aumenta la potenza dissipata)
Potenza associata alla carica/scarica del condensatore |
Questa volta poniamo tr{displaystyle t_{r}}


Adesso la potenza dissipata sarà quella utilizzata dai MOS per caricare e scaricare il condensatore.
Possiamo identificare 3 parametri:
Pc{displaystyle P_{c}}= potenza dissipata dal condensatore (in un periodo si sarà caricato e scaricato, quindi avrà assorbito e ceduto la stessa potenza; questo porta ad avere una potenza media dissipata nulla
Pn=Idn(t)∗Vdsn(t){displaystyle P_{n}=I_{dn}(t)*V_{dsn}(t)}- Potenza dissipata dal N-MOS per scaricare il condensatore
Pp=Idp(t)∗Vsdn(t){displaystyle P_{p}=I_{dp}(t)*V_{sdn}(t)}- Potenza dissipata dal P-MOS per caricare il condensatore
Quindi la potenza media dinamica è
- ⟨Pd⟩=Pn+Pp+Pc=Pn+Pp {displaystyle langle P_{d}rangle =P_{n}+P_{p}+P_{c}=P_{n}+P_{p} }
Note |
^ Arriva un nuovo tipo di sensore CMOS
Voci correlate |
- MOSFET
- Logica NMOS
- Logica PMOS
- Invertitore
- Dispositivo a carica accoppiata
- Serie 4000
Altri progetti |
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su CMOS
Wikimedia Commons contiene immagini o altri file su CMOS
Collegamenti esterni |
- CMOS, in Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana, 15 marzo 2011.
.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}
dNPf9,mZEhGVG4pNqXb,VIYz rZ1vPxr2Z5 uaUKXa


![langle P_d rangle = frac {1}{T} left [ int_{t_a}^{t_b} P_d operatorname dt + int_{t_b}^{t_c} P_d operatorname dt + int_{t_d}^{t_e} P_d operatorname dt + int_{t_e}^{t_f} P_d operatorname dt right ] =](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb8a552bbde9317d4e7e4dae0ac306663bb1e18)
![= frac {V_{dd}}{T} left [ int_{t_a}^{t_b} I_{dn,sat}(t) operatorname dt + int_{t_b}^{t_c} I_{dp,sat}(t) operatorname dt + int_{t_d}^{t_e} I_{dp,sat}(t) operatorname dt + int_{t_e}^{t_f} I_{dn,sat}(t) operatorname dt right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5be454346637de58f81ffb4fc7cba6fd860f3e6)



![langle P_d rangle= frac {4 V_{dd}}{T} left [ int_{t_a}^{t_b} frac {beta_n}{2} (V_{gsn}(t) - V_{tn})^2 operatorname dt right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb18f575f260ca69e6f24d5b099ffddd0b9ed27)



![langle P_d rangle = beta * t_r * frac {V_{dd}^3}{12 T} left [ 1 - frac {2V_{tn}}{V_{dd}} right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fda695cdbb08266eea5cd1c9d3c64afb61e5cbf2)



