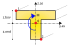
Sforzo di taglio

Multi tool use

Esempio di sforzo di taglio e conseguente deformazione.
In fisica lo sforzo di taglio (o sforzo tangenziale) è uno degli sforzi elementari cui può essere soggetto un corpo, insieme allo sforzo normale, e si misura pertanto in Pa. Viene spesso indicato con il simbolo τ o τs, nella statica applicata all'edilizia si indica solitamente con la lettera V (maiuscola).[1]
La composizione di sforzi di taglio e sforzi normali può dare luogo a flessione, mentre la composizione di più sforzi di taglio può dare luogo a torsione.
Indice
1 Lo sforzo di taglio nei materiali solidi
1.1 Il taglio come tensione fittizia
1.2 Il taglio nei chiodi e bulloni
1.3 Taglio e flessione nelle travi
1.4 Sezione resistente
2 Fluidi newtoniani
2.1 Test di laboratorio
3 Note
4 Voci correlate
5 Collegamenti esterni
Lo sforzo di taglio nei materiali solidi |
Nei materiali solidi lo sforzo di taglio è uno stato di tensione in cui la forma di un materiale tende a cambiare (di solito per forze interne di scorrimento trasversali) senza cambiamenti di volume (nel caso di materiali elasto-lineari e isotropi).
Il cambiamento di forma è quantificato misurando la variazione relativa dell'angolo tra i lati inizialmente perpendicolari di un elemento differenziale del materiale (deformazione di taglio). Una definizione semplice di sforzo di taglio rappresenta questo come componenti della tensione a un punto che agisce parallelamente al piano su cui esse giacciono.
Nei solidi cristallini ad esempio si può risalire allo sforzo di taglio necessario per attivare lo scorrimento dei piani. Quest'ultimo è detto CRSS ed è un valore caratteristico per ogni monocristallo reale. Il CRSS è lo sforzo necessario ad innescare la deformazione di taglio (parallelamente quindi al piano preso in considerazione). Sperimentalmente si ricava che lo sforzo necessario ad innescare la deformazione plastica in un monocristallo reale è inferiore al valore teorico (monocristallo ideale) ricavato.
Τn < Τmax , questo perché un monocristallo reale presenta difetti che agevolano lo sforzo.
Il taglio come tensione fittizia |
Come riportato da Fritz Leonhardt[2] nelle strutture agiscono effettivamente solo tensioni di trazione e compressione.
Le tensioni di taglio sono state introdotte nelle teorie classiche della scienza delle costruzioni perché tali teorie, per semplicità di calcolo, fanno riferimento a un sistema cartesiano x,y,z lungo il quale vengono scomposte le tensioni principali effettivamente agenti (nella teoria delle travi inflesse si hanno ad esempio σx τyz e τzy).
Tale concetto è alla base del traliccio di Ritter-Mörsch nel quale il comportamento flessionale di una trave viene studiato mediante un traliccio costituito da soli tiranti e puntoni.
Tale ipotesi ha avuto un'evoluzione recente con il metodo tirante e puntone.
Il taglio nei chiodi e bulloni |
In questo caso la sollecitazione di taglio agisce nel gambo del chiodo e/o sul cilindro filettato del bullone (vite). La formula si applica in modo semplificato, ipotizzando che vi sia una distribuzione uniforme delle tensioni tangenziali:
- τs=FtA{displaystyle tau _{s}={frac {F_{t}}{A}}}
Ft è la forza tagliante (N)
A è l'area della sezione di taglio, che può non essere la sezione nominale del pezzo (se espressa in mm2, lo sforzo risulterà in MPa)
Il principio della resistenza a taglio nei chiodi o bulloni fu scoperto da Galileo Galilei e illustrato nel trattato Due nuove scienze del 1638 (giornata 1 - paragrafo 5).
Taglio e flessione nelle travi |

Una trave prima e dopo l'applicazione di una forza
Le sollecitazioni di Flessione e Taglio all'interno delle travi sono sempre presenti contemporaneamente. Le formule matematiche delle due sollecitazioni sono correlate fra loro, in quanto il Taglio è la derivata prima della Flessione.
- Ft(z)=dMf(z)dz⇒Mf(z)=∫Ft(z)dz{displaystyle {F_{t}(z)}={frac {dM_{f}(z)}{dz}}Rightarrow M_{f}(z)=int F_{t}(z),dz}
Mf è il momento flettente (Nm)
z è la lunghezza del concio della trave (m);
Lo sforzo di taglio puro, applicato su una trave, può essere rappresentato con due forze di direzione verticale uguali in modulo, con punti di applicazione molto vicini tra loro. La flessione è pressoché annullata dal fatto che il braccio di leva tra le due forze è quasi nullo.
La deformazione di tipo tagliante, se non adeguatamente contrastata, tende a far assumere alla trave una forma a "Z", provocando un'alterazione locale all'asse della trave.
Dopo gli esperimenti sulla rottura dei materiali svolti nel Seicento e Settecento, fu sviluppata un modello matematico dagli ingegneri francesi Navier e De Saint-Venant nell'Ottocento. Questa difficile teoria matematica fu semplificata in base alle ricerche svolte da Jourawski sulla resistenza a taglio nei ponti metallici ferroviari: nella sua teoria semplificata la sezione ove è applicata l'azione tagliante è soggetta a uno scorrimento trasversale, con la generazione di tensioni tangenziali, e le tensioni si calcolano con la formula di Jourawski, di tipo τ{displaystyle {tau }}
- τs=FtSIb{displaystyle tau _{s}={frac {F_{t}S}{Ib}}}
Ft è la forza tagliante [N]
S momento statico (rispetto all'asse baricentrico) di una delle due parti di sezione individuate dalla dividente parallela all'asse baricentrico nel punto dove si calcola la tensione tangenziale (mm3)
I momento di inerzia (rispetto all'asse neutro) della sezione (mm4)
b larghezza della corda nel punto considerato (mm)
Sezione resistente |
Progettare una sezione che resista bene a taglio, data una certa configurazione di carico, implica:
- scegliere un materiale di qualità idonea all'applicazione, in grado di sopportare una τ{displaystyle {tau }}
adeguata.
- dimensionare adeguatamente la geometria della sezione (b, S, J, A) dipendono da questa scelta.
Nella pratica, una trave in acciaio, con sezione a T, cioè caratterizzata da una larga piattabanda e una lunga anima, per resistere bene a flessione, può essere soggetta a problemi per taglio poiché lo spessore dell'anima risulta troppo sottile.
Una trave rettangolare in cemento armato, di geometria definita con larghezza b e altezza h, resiste al taglio in maniera più complicata. Se gli sforzi di taglio sono lievi le armature metalliche saranno dimensionate per la sola flessione. Se gli sforzi di taglio sono rilevanti si effettua un calcolo dell'armatura a taglio, ovvero staffe e ferri piegati, in modo da verificare la resistenza alle configurazioni di carico di progetto.
Fluidi newtoniani |

Rappresentazione degli sforzi tangenziali agenti su un fluido newtoniano.
Per calcolare l'entità degli sforzi tangenziali all'interno di un fluido si fa riferimento a due straterelli piani paralleli alla parete, uno fisso e uno mobile, separati da uno spessore differenziale normale alla parete.
La legge di Newton (in ambiente anglosassone nota come legge di Stokes) afferma che lo sforzo tangenziale τij{displaystyle tau _{ij}}
- τij=−μ∂vi∂rj{displaystyle tau _{ij}=-mu {frac {partial {v_{i}}}{partial {r_{j}}}}}
essendo:
μ{displaystyle mu }la viscosità del fluido
dvi{displaystyle dv_{i}}la differenza di velocità tra i due straterelli di fluido lungo la direzione i.
drj{displaystyle dr_{j}}la differenza di posizione tra i due straterelli di fluido lungo la direzione j perpendicolare a i.
In genere si ha la presenza di sforzi o tensioni o pressioni di taglio nei fluidi viscosi, come gli oli lubrificanti e simili. I fluidi per i quali questi sforzi seguono la legge di Newton sono detti newtoniani. Quando gli sforzi o pressioni di Taglio sono assenti, il fluido viene chiamato fluido perfetto.
Test di laboratorio |
Nei test di laboratorio lo sforzo di taglio viene ottenuto tramite torsione di un provino. Un'azione trasversale diretta a un provino, causata da un momento, induce uno sforzo di taglio, ma anche sollecitazioni di trazione e di compressione.
I componenti strutturali che sopportano lo sforzo di taglio, in un'automobile, sono le barre di torsione e l'albero motore.
I giunti bullonati e rivettati possono essere anch'essi soggetti a uno sforzo prevalentemente trasversale. Le travi d'appoggio, le leve nei quadri comando, le teste delle colonne sono soggette a un carico composto che consiste nello sforzo di taglio, di trazione e di compressione.
Anche le costruzioni sul suolo possono avere dei problemi a causa delle deformazioni trasversali; per esempio il peso di una diga riempita di terra o muro di contenimento potrebbe fare collassare il sottosuolo con piccoli smottamenti.

Una strada distrutta da una frana del terreno
I vettori dello sforzo di taglio sono rilevanti nel determinare come i fluidi scorrono sulle superfici, poiché essi generano uno sfregamento interno tra filetti fluidi. In particolare, il flusso laminare sulla superficie ha una velocità nulla e ciò genera un gradiente o differenziale di scorrimento rispetto alla corrente più interna del liquido.
Lo sforzo di taglio ha importanza biologica nel caso del flusso sanguigno. Le cellule endoteliali riconoscono gli sforzi di taglio e trasducono dei segnali alle cellule muscolari dei vasi e ad altre cellule in modo da modificare la struttura dei vasi. Questo adattamento è necessario perché le regioni a elevato sforzo di taglio dei vasi devono avere pareti più spesse.
Note |
^ Dall'inglese shear, per distinguerlo dalla torsione τt
^ F.Leonhardt - E Monning - Le basi del dimensionamento nelle costruzioni in cemento armato - ETS
^ .mw-parser-output .chiarimento{background:#ffeaea;color:#444444}.mw-parser-output .chiarimento-apice{color:red}
http://www.treccani.it/export/sites/default/Portale/sito/altre_aree/scienze_della_terra/enciclopedia/italiano_vol_5/223_248__x4_2_Fenomeni_x_ita.pdf[collegamento interrotto]
Voci correlate |
- Modulo di taglio
- Geotecnica
- Modulo di elasticità
- Tenacità
- Resilienza (ingegneria)
- Trazione (fisica)
- Meccanica del continuo
- Taglio nel cemento armato
- Viscosità
- Centro di taglio (fisica)
Collegamenti esterni |
- (EN) IUPAC Gold Book, "shear strain", su goldbook.iupac.org.
.mw-parser-output .CdA{border:1px solid #aaa;width:100%;margin:auto;font-size:90%;padding:2px}.mw-parser-output .CdA th{background-color:#ddddff;font-weight:bold;width:20%}
| Controllo di autorità | GND (DE) 4191822-8 |
|---|
B2,52MrZlUadwUHHp4mIZ z,O,cViFGLJ2G6HzrT8 MXyF4wXI2eWc