Gfrktyl

Un iperboloide, un cilindro e una sfera: si tratta di superfici con curvatura gaussiana (rispettivamente) negativa, nulla e positiva.

In geometria differenziale, la curvatura gaussiana è una misura della curvatura di una superficie in un punto.

La curvatura gaussiana in un punto x{displaystyle x} di una superficie contenuta nello spazio euclideo è definita come il prodotto delle due curvature principali in x{displaystyle x}. La curvatura gaussiana, a differenza delle curvature principali, è una curvatura intrinseca: dipende cioè soltanto dalle distanze fra punti all'interno della superficie, e non da come questa sia contenuta nello spazio tridimensionale. Questo fatto importante è asserito dal teorema egregium di Gauss.

Un altro tipo di curvatura calcolato a partire dalle curvature principali è la curvatura media. A differenza della curvatura di Gauss, la curvatura media non è intrinseca.

Definizione |

Hessiano |

Una semplice definizione della curvatura gaussiana di una superficie è la seguente. La curvatura gaussiana non cambia se la superficie viene spostata con movimenti rigidi. Per definire la curvatura gaussiana di una superficie X{displaystyle X} in un punto P{displaystyle P}, possiamo quindi ruotare X{displaystyle X} in modo che il piano tangente in P{displaystyle P} sia orizzontale. A questo punto la superficie è descritta (almeno localmente, in un intorno di P{displaystyle P}) come grafico di una funzione

f:A→R{displaystyle f:Ato mathbb {R} }

avente come dominio un aperto A{displaystyle A} di R2{displaystyle mathbb {R} ^{2}}. La curvatura gaussiana in P=(x,y,f(x,y)){displaystyle P=(x,y,f(x,y))} è il determinante dell'hessiano di f{displaystyle f} in (x,y){displaystyle (x,y)}. Perché questa definizione abbia senso, la funzione deve essere differenziabile almeno due volte: l'hessiano è infatti la matrice simmetrica 2×2{displaystyle 2times 2} data dalle derivate parziali seconde di f{displaystyle f}.

Curvature principali |

La curvatura gaussiana di una superficie più generale X{displaystyle X} in un punto x{displaystyle x} è il prodotto k1k2{displaystyle k_{1}k_{2}} delle curvature principali. Per definire le curvature principali è necessario fissare una normale alla superficie in X{displaystyle X}: poiché la normale opposta dà curvature con segni opposti, il loro prodotto è però ben definito anche senza questa scelta.

Esempi |

Curvatura costante |

Un piano o un cilindro hanno curvatura gaussiana ovunque nulla. Una sfera di raggio r{displaystyle r} ha curvatura gaussiana ovunque 1/r2{displaystyle 1/r^{2}}.

Esempio puntuale |

Il paraboloide f(x,y)=x2+y2{displaystyle f(x,y)=x^{2}+y^{2}} ha curvatura positiva nel suo punto di minimo, pari al determinante dell'hessiano. Ha curvatura positiva anche negli altri punti, ma con valore differente dal determinante.

La funzione

f(x,y)=ax2+by2{displaystyle f(x,y)=ax^{2}+by^{2}}

ha gradiente (2ax,2by){displaystyle (2ax,2by)}. Il gradiente è nullo nell'origine, e quindi la curvatura gaussiana del grafico X{displaystyle X} di f{displaystyle f} in (0,0){displaystyle (0,0)} è il determinante dell'hessiano. L'hessiano è

(2a002b){displaystyle {begin{pmatrix}2a&0\0&2bend{pmatrix}}}

ed il suo determinante è 4ab{displaystyle 4ab}. La curvatura di X{displaystyle X} in (0,0){displaystyle (0,0)} è quindi 4ab{displaystyle 4ab}. Questa è ad esempio negativa in presenza di un punto di sella, ove a{displaystyle a} e b{displaystyle b} hanno segni discordi.

Questo metodo per calcolare la curvatura è però funzionante solo in (0,0){displaystyle (0,0)}, dove il gradiente si annulla.

Curvatura totale |

La somma degli angoli di un triangolo su una superficie di curvatura negativa è minore di quella che si ottiene su un triangolo piano (cioè π{displaystyle pi }).

La curvatura totale di una regione A{displaystyle A} della superficie X{displaystyle X} è l'integrale di superficie

∫AKds{displaystyle int _{A}K,ds}

della curvatura gaussiana K{displaystyle K} su A{displaystyle A}. La curvatura totale misura quanto si differenzia globalmente la geometria di A{displaystyle A} da quella di una regione piatta sul piano: ad esempio, la curvatura totale di un triangolo geodetico T{displaystyle T} è pari alla differenza fra la somma dei suoi angoli interni (in radianti) e π{displaystyle pi }. In altre parole,

∑i=13θi=π+∫TKds{displaystyle sum _{i=1}^{3}theta _{i}=pi +int _{T}K,ds}

dove θ1,θ2{displaystyle theta _{1},theta _{2}} e θ3{displaystyle theta _{3}} sono gli angoli interni.

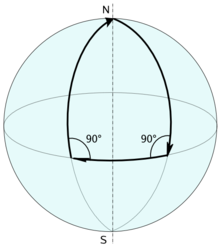
La somma degli angoli di un triangolo su una sfera, che ha curvatura positiva, è maggiore di π{displaystyle pi }.

La somma degli angoli di un triangolo su una superficie di curvatura ovunque positiva è maggiore di π{displaystyle pi }, mentre è minore se la superficie ha curvatura ovunque negativa.

Proprietà |

Teorema egregium |

Per il teorema egregium dimostrato da Gauss nel 1828, la curvatura gaussiana dipende solo dalla sua prima forma fondamentale, cioè dal suo tensore metrico.

La curvatura gaussiana è quindi invariante per isometrie della superficie: si tratta cioè di una proprietà intrinseca della superficie. Una isometria non è necessariamente un movimento rigido dello spazio: un esempio è fornito da un foglio di carta, che può essere arrotolato fino a formare un cilindro. Piano e cilindro sono (almeno localmente) isometrici.

Gauss-Bonnet |

Il teorema di Gauss-Bonnet fornisce una stretta connessione fra la curvatura totale di una superficie e la sua topologia. Se X{displaystyle X} è una superficie compatta, il teorema asserisce che

∫XKds=2πχ(X){displaystyle int _{X}K,ds=2pi chi (X)}

cioè la curvatura totale della superficie è pari alla sua caratteristica di Eulero, moltiplicata per 2π{displaystyle 2pi }.

Ad esempio, una sfera di raggio r{displaystyle r} ha caratteristica 2, e la sua curvatura totale è sempre 4π{displaystyle 4pi }, indipendentemente da r{displaystyle r}. Infatti, è pari al prodotto fra l'area 4πr2{displaystyle 4pi r^{2}} e la curvatura, che è costantemente pari a 1/r2{displaystyle 1/r^{2}}, poiché entrambe le curvature principali sono 1/r{displaystyle 1/r}. Più sorprendentemente, la curvatura totale di una qualsiasi superficie omeomorfa alla sfera (ad esempio, il bordo di un ellissoide) è sempre 4π{displaystyle 4pi }.

I punti più esterni di un Toro hanno curvatura positiva, quelli più interni negativa, e si compensano in modo che l'integrale sulla superficie sia nullo.

Un toro ha caratteristica di Eulero nulla. Ne segue che la sua curvatura totale è nulla: o questa è ovunque nulla (cosa però impossibile per un toro contenuto nello spazio tridimensionale), oppure presenta zone di curvatura positiva e zone di curvatura negativa.

Bibliografia |

• (EN) Manfredo do Carmo, Differential Geometry of Curves and Surfaces, 1976, ISBN 0-13-212589-7.

Voci correlate |

• Curvatura principale


• Teorema egregium


• Teorema di Gauss-Bonnet


• Teorema di uniformizzazione di Riemann

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica