Gfrktyl

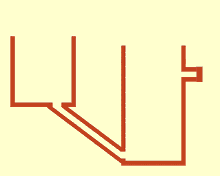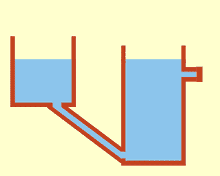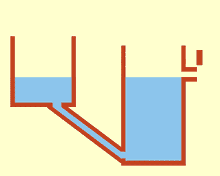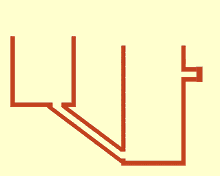
Rappresentazione del principio dei vasi comunicanti.

Il principio dei vasi comunicanti è il principio fisico secondo il quale un liquido contenuto in due o più contenitori comunicanti tra loro, in presenza di gravità, raggiunge lo stesso livello originando un'unica superficie equipotenziale.

Dimostrazione |

Questa voce o sezione sull'argomento fisica è ritenuta da controllare. Motivo: Lo studio del sistema è fatto in modo approssimativo Partecipa alla discussione e/o correggi la voce. Segui i suggerimenti del progetto di riferimento.

Questa voce o sezione sull'argomento fisica non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento.

Se ai capi dei vasi comunicanti troviamo due liquidi differenti non miscibili e indichiamo con ρ₁ e ρ₂ la densità dei due liquidi, h₁ e h₂ la loro altezza, P₁ e P₂ la pressione che essi esercitano e indichiamo con g la gravità e p_A la pressione atmosferica si ha:

P1=P2{displaystyle P_{1}=P_{2}}

e in base alla legge di Stevino:^[1]

ρ1⋅g⋅h1+pA=ρ2⋅g⋅h2+pA{displaystyle rho _{1}cdot gcdot h_{1}+p_{A}=rho _{2}cdot gcdot h_{2}+p_{A}}

ρ1⋅h1=ρ2⋅h2{displaystyle rho _{1}cdot h_{1}=rho _{2}cdot h_{2}}

Si noti che nell'ultima equazione il prodotto ρ[kgm3]⋅h[m]{displaystyle rho [{frac {kg}{m^{3}}}]cdot h[m]} al primo e secondo membro indica la densità superficiale del liquido ([kg / m²]).

La proprietà dei vasi comunicanti è un caso particolare, nel quale si considera un solo liquido e l'equazione si riduce alla seguente forma: h1=h2{displaystyle h_{1}=h_{2}}.

Se consideriamo un bacino e il caso di un solo liquido, sono dati: l'altezza del liquido nel bacino h1{displaystyle h_{1}} (oppure h2{displaystyle h_{2}}), la gravità g{displaystyle g} e le densità ρ1{displaystyle rho _{1}} e ρ2{displaystyle rho _{2}}. Collegato il bacino ad altri vasi, la profondità h2{displaystyle h_{2}}(oppure h1{displaystyle h_{1}}) che il liquido assume nei vasi comunicanti è data ed è la stessa indipendentemente dalla forma o diametro del recipiente.

È rilevante notare che il livello del liquido non dipende dalla distanza fra i vasi (h1{displaystyle h_{1}} e h2{displaystyle h_{2}} sono le altezze del liquido nel bacino e in un vaso comunicante).

Il principio dei vasi comunicanti spiega diversi fenomeni e viene sfruttato dall'uomo per diverse applicazioni pratiche.

Se sul liquido non agiscono forze esterne, si arriva ad un equilibrio stabile nel quale il pelo libero del liquido si dispone su un piano orizzontale.

Generalizzazione |

Una formulazione alternativa e più generale del principio dei vasi comunicanti è la seguente: la superficie libera di un liquido in equilibrio idrostatico è una superficie equipotenziale del campo gravitazionale.

L'equilibrio idrostatico, infatti, si ottiene quando il liquido assume la forma che minimizza la sua energia potenziale gravitazionale complessiva: in tale forma il potenziale alla superficie deve essere uniforme; se così non fosse, spostando del liquido da una regione a potenziale più alto ad una a potenziale più basso l'energia potenziale diminuirebbe e ciò è impossibile, in quanto per ipotesi essa è già minima.

Mentre la formulazione tradizionale del principio vale soltanto nel caso di campo gravitazionale costante in intensità e direzione, approssimazione valida per piccole regioni sulla superficie terrestre, la formulazione avanzata vale qualunque sia l'espressione del campo gravitazionale e su regioni di qualunque grandezza, anche sull'intera superficie della Terra. Essa si può utilizzare per dimostrare che (trascurando l'effetto delle maree, del moto ondoso, eccetera) la superficie degli oceani coincide con il geoide.

Applicazioni |

L'uomo utilizza il principio dei vasi comunicanti per diverse applicazioni. Si riportano di seguito alcuni esempi:

Impianti idrici |

Trasporto dell'acqua negli edifici sfruttando il principio dei vasi comunicanti

È possibile far arrivare l'acqua potabile negli edifici perché il serbatoio generale dell'acqua - nelle città e nei paesi - è situato in posizione elevata e collegato, mediante i tubi della rete di distribuzione, con tutti i punti di utilizzo.

Canali artificiali |

L'acqua dei mari e degli oceani della Terra è allo stesso livello, tranne piccole differenze. Costruendo canali artificiali come il Canale di Suez o il Canale di Corinto, l'acqua riempie il canale portandosi allo stesso livello dei mari messi in comunicazione, consentendo alle imbarcazioni di navigare da una estremità all'altra del canale. Spesso tuttavia, ad esempio quando si è in presenza di forti dislivelli del terreno, si rende necessaria la costruzione di chiuse, che a loro volta funzionano in base al principio dei vasi comunicanti, come per il Canale di Panama.

Chiuse |

Una chiusa è uno sbarramento artificiale che separa due specchi d'acqua con differente livello. La funzione è consentire il passaggio di navi e imbarcazioni tra due specchi d'acqua a quote diverse, come avviene ad esempio per la navigazione del Nilo.

Pozzi di drenaggio in falda freatica |

Se si scava un pozzo, l'acqua raggiunge lo stesso livello della falda freatica circostante.
Se per mezzo di pompe si provoca un abbassamento del livello dell'acqua nel pozzo, per il principio dei vasi comunicanti anche l'acqua della falda acquifera si abbassa.

Pozzo in falda artesiana |

Nel caso di falde racchiuse tra strati superiori e inferiori impermeabili a forma di conca, la falda acquifera artesiana si trova imprigionata ed è in pressione e non a pelo libero.
Scavando un pozzo nell'area di maggiore avvallamento, l'acqua zampilla in superficie.

Travaso |

I liquidi si possono travasare da un recipiente all'altro per sifonamento. Si colloca il recipiente pieno a un livello superiore rispetto a quello da riempire. I due recipienti si mettono in comunicazione per mezzo di un tubo (detto sifone), si fa in modo - ad esempio aspirando con la bocca - che il tubo sia pieno di liquido, si immette il tubo nel recipiente da cui prelevare liquido e avviene il travaso, perché il liquido nel recipiente posto più in basso cerca di raggiungere lo stesso livello di quello posto più in alto.
L'applicazione ha un uso nel travaso del vino, dell'acqua negli acquari e dello scarico dei bagni.

Livella |

Il principio è sfruttato per ottenere uno strumento, molto semplice ma di grande precisione, atto a porre due o più punti allo stesso livello orizzontale. Costituito da un tubo flessibile alle cui estremità sono collegate due ampolle cilindriche trasparenti tenute verticali; riempiendo d'acqua il sistema fino a vedere il livello salire a metà delle ampolle, è possibile rilevare i riferimenti. Pensiamo come mettere in piano un campo sportivo in costruzione, fissata un'ampolla su un angolo e rilevato il riferimento di partenza, spostando l'altra sugli altri tre, si ha la certezza di una messa in piano dei quattro angoli.

Note |

Bibliografia |

• Enrico Turchetti, Romana Fasi, Elementi di Fisica, 1ª ed., Zanichelli, 1998, ISBN 88-08-09755-2.

Voci correlate |

• Legge di Stevino


• Torrino piezometrico

Portale Fisica

Portale Ingegneria