Gfrktyl

In chimica la tensione superficiale (generalmente indicata con la lettera greca γ) è la densità superficiale di energia di legame sull'interfaccia tra un corpo continuo e un materiale di un'altra natura, ad esempio un solido, un liquido o un gas. Non è quindi assimilabile dimensionalmente ad una tensione (definita invece come densità superficiale di forza): nel Sistema internazionale si misura infatti in Newton su metro (N/m).

Dal punto di vista termodinamico può essere definita come il lavoro necessario per aumentare la superficie del continuo di una quantità unitaria.^[1] Il paracoro è una grandezza che esprime il volume molare dei liquidi corretto considerando l'effetto della tensione superficiale.

Alcuni insetti, come quello nella foto, l'idrometra, sfruttano la tensione superficiale per "camminare" sull'acqua

La tensione superficiale impedisce alla moneta di affondare

Fluidodinamica |

La tensione superficiale è definibile nel modo più elementare dal punto di vista meccanico come la forza per unità lineare che tiene uniti i lembi di un ipotetico taglio praticato perpendicolarmente alla superficie libera del fluido, ovvero:

γ=dFSdl{displaystyle gamma ={frac {d{textbf {F}}_{S}}{dl}}},

dove dl{displaystyle dl} è la lunghezza di un tratto infinitesimo del taglio e dFS{displaystyle d{textbf {F}}_{S}} è la forza infinitesima perpendicolare al taglio e giacente sulla superficie.

Si può ricavare la stessa definizione tenendo conto del fatto che una lamina liquida tende spontaneamente a raggiungere la configurazione di minima superficie, per cui la tensione superficiale si definisce come:

γ=dWdA{displaystyle gamma ={frac {dW}{dA}}}

dove dW{displaystyle dW} è il lavoro elementare compiuto contro le forze di tensione superficiale per ottenere un aumento infinitesimo dA{displaystyle dA} della superficie della lamina.

Bagnabilità |

Una goccia su una superficie con bassissima bagnabilità assume una forma sferoidale, con un solo punto di contatto con la superficie solida.

Nel momento in cui si dovesse tenere conto di ciò che si trova al di fuori del liquido, non è più sufficiente considerare le sole forze di coesione, in quanto la presenza di un altro corpo ha influenza sui valori della tensione, nel senso che le molecole di questo svolgono anch'esse delle azioni (le forze di adesione) sulle molecole dello strato superficiale del liquido. In effetti, per ragioni del tutto simili a quelle sopra indicate, anche la superficie dei solidi possiede tensioni superficiali, ma a causa della mancanza di mobilità della superficie questa non è direttamente osservabile, né misurabile con metodi diretti.

Quando liquido e solido vengono in contatto, quindi, a causa delle interazioni tra le differenti fasi viene a stabilirsi una tensione interfacciale definita come l'energia addizionale per unità di area dovuta alla formazione di una interfaccia (supponendo anche la presenza di un gas) solido/liquido e solido/gas.

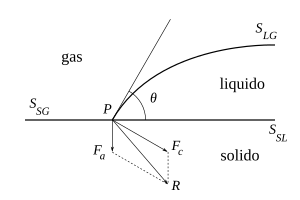
Il profilo di una porzione di liquido posta su di una superficie solida formerà con essa un angolo θ{displaystyle theta } (vedere figure) che sarà maggiore o minore dell'angolo retto a seconda che in P{displaystyle P} prevalga in modulo il risultante delle forze di coesione, Fc{displaystyle F_{c}}, (normale alla tangente al profilo del liquido in P{displaystyle P} e rivolto verso l'interno), oppure il risultante delle forze di adesione, Fa{displaystyle F_{a}}, (normale alla superficie solida rivolto verso di essa).

Dette SLG{displaystyle S_{LG}}, SSL{displaystyle S_{SL}} e SSG{displaystyle S_{SG}}, rispettivamente le superfici di separazione liquido/gas, solido/liquido e solido/gas, e indicate con γLG{displaystyle gamma _{LG}}, γSL{displaystyle gamma _{SL}}, γSG{displaystyle gamma _{SG}} le loro energie libere, l'energia libera totale è:

F=γLG⋅SLG+γSL⋅SSL+γSG⋅SSG.{displaystyle F=gamma _{LG}cdot S_{LG}+gamma _{SL}cdot S_{SL}+gamma _{SG}cdot S_{SG}.}

Il liquido si dispone in modo da minimizzare l'energia libera totale delle superfici (è trascurabile, per piccoli volumi, il termine gravitazionale dell'energia ρ⋅V⋅g⋅zG{displaystyle rho cdot Vcdot gcdot z_{G}} rispetto a quello superficiale γLG⋅S{displaystyle gamma _{LG}cdot S}). Un'utile espressione dell'angolo di contatto θ{displaystyle theta } è fornita dalla condizione di equilibrio, data dall'equazione di Young:

γLGcos⁡(θ)=(γS−γSL)−(γS−γSG)≅γSG−γSL.{displaystyle gamma _{LG}cos(theta )=(gamma _{S}-gamma _{SL})-(gamma _{S}-gamma _{SG})cong gamma _{SG}-gamma _{SL}.}

Soltanto γ{displaystyle gamma } e θ{displaystyle theta } sono determinabili sperimentalmente, si trovano tuttavia nella letteratura scientifica delle relazioni sperimentali per il calcolo di γS{displaystyle gamma _{S}} e γSL{displaystyle gamma _{SL}}, come ad esempio la legge di Girifalco e Good (1957-60):

γSL=γS+γLG−2ϕ⋅γS⋅γLG,{displaystyle gamma _{SL}=gamma _{S}+gamma _{LG}-2phi cdot {sqrt {gamma _{S}cdot gamma _{LG}}},}

con

ϕ=4VS⋅VL3(VS3+VL3)2{displaystyle phi ={frac {4{sqrt[{3}]{V_{S}cdot V_{L}}}}{({sqrt[{3}]{V_{S}}}+{sqrt[{3}]{V_{L}}})^{2}}}}

e VS{displaystyle V_{S}} e VL{displaystyle V_{L}} volumi molari di solido e liquido.

Le condizioni limite θ=0{displaystyle theta =0} e θ=π{displaystyle theta =pi } esprimono rispettivamente:

• bagnabilità completa con la formazione di uno strato di liquido di spessore molecolare;


• totale assenza di bagnabilità.

In conclusione, la bagnabilità, favorita da basse energie interfacciali, elevate energie superficiali γS{displaystyle gamma _{S}} e modeste tensioni superficiali, a parità di liquido bagnante (γLG{displaystyle gamma _{LG}}) e di tipo di materiale solido, risulta fortemente influenzata dallo stato di levigatezza e dalla presenza di impurità sulla superficie del materiale stesso: ciò è osservabile sperimentalmente anche sotto forma di menisco.

Alcuni valori |

Considerando liquidi a contatto con l'aria con una temperatura 20 °C, la tensione superficiale sarà:

Termodinamica |

Goccia d'acqua danzante su una superficie d'acqua soggetta a vibrazioni, in modo da conservare la tensione superficiale ed evitare la fusione con la superficie d'acqua

Le azioni attrattive tra le molecole di un liquido (le forze di coesione) fanno sì che le molecole dello strato superficiale siano soggette a una forza risultante non nulla che tende a farle spostare verso l'interno; esse pertanto tendono a sfuggire dalla superficie limite del liquido e di conseguenza questa tende ad assumere la estensione minima possibile (in assenza di altre forze, la superficie minima, è quella sferica).

Le molecole sulla superficie possiedono una energia potenziale superiore a quella delle molecole all'interno del liquido, sicché se si vuole aumentare la estensione della superficie libera di un liquido occorre spendere un'energia proporzionale all'aumento di superficie.

Se il liquido viene sottoposto a una trasformazione che alteri esclusivamente la sua superficie S{displaystyle S}, si ha una variazione dell'energia interna, ΔU{displaystyle Delta U}, che è praticamente pari alla variazione di energia potenziale dello strato superficiale, e quindi proporzionale all'incremento ΔS{displaystyle Delta S} della superficie. Tale variazione di energia interna (per il Primo principio della termodinamica) è in parte (Q{displaystyle Q}) fornita dall'energia cinetica delle molecole dell'ambiente e in parte (L{displaystyle L}) corrispondente a un lavoro meccanico che deve essere fornito dall'esterno.

Si definisce tensione superficiale (o energia libera superficiale) di un liquido la quantità di lavoro richiesto per aumentare la estensione della sua superficie di una unità mantenendo costante la temperatura del sistema, cioè l'aumento di energia libera per unità di superficie:

γ=(∂G∂A)P,T{displaystyle gamma =left({frac {partial G}{partial A}}right)_{P,T}},

dove G{displaystyle G} è l'energia libera di Gibbs e A{displaystyle A} è la superficie.

Da ciò è possibile dedurre la prima equazione di Kelvin che fornisce l'entalpia superficiale (o energia superficiale) HA=γ−T(∂γ∂T)P{displaystyle H^{A}=gamma -Tleft({frac {partial gamma }{partial T}}right)_{P}}

Influenza della temperatura sulla tensione superficiale |

Esistono solo relazioni empiriche per determinare l'influenza della temperatura sul valore assunto dalla tensione superficiale.

Eötvös |

γV2/3=k(TC−T){displaystyle gamma V^{2/3}=k(T_{C}-T)}

in cui:

• 
  V{displaystyle V} è il volume molare della sostanza


• 
  TC{displaystyle T_{C}} è la temperatura critica


• 
  k{displaystyle k} è costante per ciascuna sostanza.

Ad esempio, per l'acqua k = 1,03 erg/°C, V= 18 ml/mol e T_C= 374 °C.

Guggenheim-Katayama |

γ=γo(1−TTC)n{displaystyle gamma =gamma ^{o}left(1-{frac {T}{T_{C}}}right)^{n}}

in cui γo{displaystyle gamma ^{o}} è una costante di ciascun liquido e n{displaystyle n} è un fattore empirico, il cui valore è 11/9 per i liquidi organici.

Salto di pressione attraverso una superficie curva |

In assenza di viscosità, il salto di pressione attraverso una superficie curva è dato dall'equazione di Young-Laplace, che pone in relazione la pressione all'interno di un liquido con la pressione esterna, la tensione superficiale e la geometria della superficie.

ΔP=γdAdV{displaystyle Delta P=gamma {frac {dA}{dV}}}.

Tale equazione è applicabile a qualsiasi superficie:

• per una superficie piana dAdV=0{displaystyle {frac {dA}{dV}}=0}: pressione interna ed esterna si equivalgono;


• per una superficie sferica PI=PO+2γR{displaystyle P_{I}=P_{O}+{frac {2gamma }{R}}}
  


• per una superficie toroidale PI=PO+γ(1R+1r){displaystyle P_{I}=P_{O}+gamma left({frac {1}{R}}+{frac {1}{r}}right)}, dove r e R sono i raggi del toroide.

Per una bolla sferica reale il termine dovuto alla tensione superficiale è doppio. Ciò è dovuto alla presenza di due superfici, una interna e una esterna alla bolla.

Seconda equazione di Kelvin |

La seconda equazione di Kelvin è ottenibile utilizzando l'Equazione di Clapeyron; essa evidenzia come, a causa della tensione superficiale, la tensione di vapore di piccole gocce di liquido in sospensione sia superiore alla tensione di vapore "standard" dello stesso liquido disposto in uno strato piano.

Pvfog=PvoeV2γrRT{displaystyle P_{v}^{fog}=P_{v}^{o}e^{frac {V2gamma }{rRT}}}

dove:

• 
  Pvo{displaystyle P_{v}^{o}} è la tensione di vapore standard di un determinato liquido a una data temperatura e pressione.


• 
  V{displaystyle V} rappresenta il volume molare.


• 
  r{displaystyle r} è il raggio della sfera.


• 
  R{displaystyle R} è la costante dei gas.

Note |

Bibliografia |

• 
  Trattato teorico e pratico di idromeccanica. v.1, Donato Spataro, U. Hoepli, Milano, 1915.


• 
  Fisica Statistica, Landau L. D., Lifšic E. M., Editori Riuniti, Roma, 1978.


• (EN) Fluid mechanics, Landau L.D., Lifshitz E.M., Pergamon Press, 1959.


• Duilio Citrini, Giorgio Noseda, Idraulica, Cesano Boscone, Casa Editrice Ambrosiana, 1987, p. 468.

Voci correlate |

• Menisco (fisica)


• Superficie minima


• Paracoro


• Capillarità


• Sforzo normale


• Sforzo di taglio


• Deformazione

Altri progetti |

• 
  Wikimedia Commons contiene immagini o altri file su tensione superficiale
  

Collegamenti esterni |

• 
  


• 
  Tensione superficiale, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
  


• Tensione superficiale (PDF), su polymertechnology.it.


• Flusso di Marangoni, su strangepaths.com.


• Video che mostra gli effetti della tensione superficiale., su fisica.decapoa.altervista.org.


• Tensioni superficiali di liquidi, su itchiavari.org.


• (EN) Tensione interfacciale (PDF), su gtdbernoulli.nl.


• (DE) Adesione (PDF), su sundoc.bibliothek.uni-halle.de.

Portale Chimica

Portale Fisica