Bottiglia di Klein

La bottiglia di Klein.
In matematica, la bottiglia di Klein (detta anche otre di Klein) è una superficie non-orientabile, cioè una superficie per la quale non c'è distinzione fra "interno" ed "esterno". La bottiglia di Klein è stata descritta per la prima volta nel 1882 dal matematico tedesco Felix Klein. È strettamente correlata al nastro di Möbius e alle immersioni del piano proiettivo reale come la superficie di Boy.
Indice
1 Descrizione informale
1.1 La bottiglia
1.2 Il quadrato
2 Proprietà
3 Parametrizzazione
4 Voci correlate
5 Altri progetti
6 Collegamenti esterni
Descrizione informale |
La bottiglia |
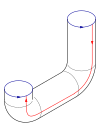
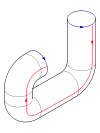
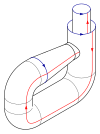
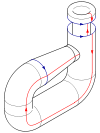
Si immagini una bottiglia con un buco sul fondo. Ora si estenda il collo della bottiglia, curvandolo su se stesso, fino ad inserirlo lateralmente all'interno di questa. Questa operazione richiede nello spazio tridimensionale che il collo perfori la parete della bottiglia: effettuata però nello spazio euclideo quadridimensionale R4{displaystyle mathbb {R} ^{4}}
Diversamente da un bicchiere, questo oggetto non ha "bordi" dove la superficie termina bruscamente.
Il nome Bottiglia di Klein pare essere nato da una traduzione errata del termine tedesco Fläche che significa superficie. Questo è stato confuso con la parola Flasche che significa bottiglia. Ciò nonostante, il nome è considerato corretto anche in tedesco.
Il quadrato |
La costruzione appena abbozzata può essere resa più rigorosa dal punto di vista geometrico, con le tecniche della topologia. La bottiglia di Klein è lo spazio topologico ottenuto identificando i bordi opposti del quadrato mostrato in figura, secondo l'orientamento data dalle frecce.
Incollando i lati secondo le due frecce rosse, si ottiene la superficie verticale di un cilindro. I lati rimanenti sono a questo punto diventati due circonferenze, che vanno identificate lungo le frecce blu. Il risultato è una bottiglia di Klein.
Dal punto di vista topologico, non è necessario effettuare manualmente tutte le identificazioni per definire o studiare la bottiglia di Klein: questa è effettivamente ben definita dalla descrizione iniziale, quella di un quadrato con una certa legge di identificazione. In topologia si dice che la bottiglia di Klein è lo spazio quoziente del quadrato, rispetto ad una certa relazione d'equivalenza.
Come molti altri spazi topologici, la bottiglia di Klein K{displaystyle K}
- f:K→R3{displaystyle f:Kto mathbb {R} ^{3}}
a valori nello spazio euclideo R3{displaystyle mathbb {R} ^{3}}
che è localmente iniettiva, ma non globalmente: due circonferenze distinte presenti in K{displaystyle K}
Proprietà |

Dividendo la bottiglia di Klein si ottiene un nastro di Möbius.
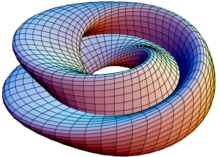
L'immersione a "figura 8" della bottiglia di Klein.
Come il nastro di Möbius, la bottiglia di Klein è una varietà differenziabile bidimensionale non orientabile. Diversamente dal nastro di Möbius, la bottiglia di Klein è una varietà chiusa, vale a dire che è una varietà compatta senza bordo. Mentre il nastro di Möbius può essere rappresentato all'interno dello spazio euclideo tridimensionale R3, la bottiglia di Klein non può (e infatti nelle rappresentazioni grafiche tridimensionali la superficie è costretta ad autointersecarsi da qualche parte) ma può essere rappresentata nello spazio euclideo quadridimensionale R4.
La bottiglia di Klein può essere costruita (in senso matematico) "incollando" i margini di due nastri di Möbius. Se una bottiglia di Klein è divisa in due lungo il suo piano di simmetria, il risultato è un nastro di Möbius, raffigurato a destra. Si tenga presente che l'intersezione raffigurata non esiste veramente. Infatti è possibile tagliare la bottiglia di Klein in un singolo nastro di Möbius.
La bottiglia di Klein ha caratteristica di Eulero pari a 0.
La bottiglia di Klein è l'unica eccezione alla congettura di Heawood, una generalizzazione del teorema dei quattro colori.
In particolare, sono sufficienti sei colori (e non quattro) per colorare una qualunque bottiglia di Klein, facendo in modo che a superfici adiacenti non venga assegnato lo stesso colore. Vedi Teorema dei quattro colori.
Parametrizzazione |
L'immersione a "figura 8" della bottiglia di Klein ha una parametrizzazione abbastanza semplice:
- x=(r+cosu2sinv−sinu2sin2v)cosu{displaystyle x=left(r+cos {frac {u}{2}}sin v-sin {frac {u}{2}}sin 2vright)cos u}
- y=(r+cosu2sinv−sinu2sin2v)sinu{displaystyle y=left(r+cos {frac {u}{2}}sin v-sin {frac {u}{2}}sin 2vright)sin u}
- z=sinu2sinv+cosu2sin2v{displaystyle z=sin {frac {u}{2}}sin v+cos {frac {u}{2}}sin 2v}
In questa immersione, il cerchio di auto-intersezione è un cerchio geometrico nel piano XY. La costante positiva r{displaystyle r}



La bottiglia di Klein prodotta con del vetro
Voci correlate |
- Topologia
- Topologia algebrica
- Superficie (matematica)
- Bottiglia di Klein solida
Altri progetti |
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su Bottiglia di Klein
Wikimedia Commons contiene immagini o altri file su Bottiglia di Klein
Collegamenti esterni |
- Alcune immagini e animazioni interattive sulla bottiglia di Klein, su matematita.it.
- (EN) Bottiglia di Klein su MathWorld, su mathworld.wolfram.com.
- (EN) Costruzione con foglio di carta, su cut-the-knot.org.
- (EN) Puzzle sulla bottiglia di Klein, su cut-the-knot.org.
- (EN) Costruzione della bottiglia di Klein (filmato avi)
- (EN) Immagini della bottiglia di Klein, di John Sullivan, su math.uiuc.edu.
- (EN) La bottiglia di Klein, su geom.uiuc.edu.
- (EN) Origami che rappresentano la bottiglia di Klein, su hektor.umcs.lublin.pl.
- (EN) Bottiglia di Klein lavorata a maglia, su toroidalsnark.net.
- Torus Games: giochi (scaricabili gratuitamente) che illustrano la topologia del toro e della bottiglia di Klein, su geometrygames.org.
.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}