Permittività elettrica
In elettromagnetismo e nella fisica dello stato solido, la permittività elettrica o permettività elettrica,[1] anche chiamata semplicemente permittività o permettività, è una grandezza fisica che descrive il comportamento di un materiale dielettrico in presenza di un campo elettrico. In particolare, quantifica la tendenza del materiale a contrastare l'intensità del campo elettrico presente al suo interno.
Indice
1 Descrizione
1.1 Definizione
2 Permittività elettrica relativa
3 Modello per la permittività elettrica
4 Dispersione e causalità
4.1 Suscettività elettrica
4.2 Permittività complessa
4.3 Polarizzazione
5 Importanza in chimica
6 Note
7 Bibliografia
8 Voci correlate
9 Collegamenti esterni
Descrizione |
La permittività elettrica è fortemente legata alla suscettività elettrica, una proprietà del materiale che ne misura la predisposizione a polarizzarsi quando viene applicato un campo elettrico. La polarizzazione di atomi e molecole produce un campo elettrico aggiuntivo nel materiale, descritto attraverso il vettore induzione elettrica, e la permittività elettrica ne quantifica l'entità per unità di carica elettrica.
Normalmente la permittività elettrica è indicata col simbolo ε{displaystyle varepsilon }
Poiché la permittività elettrica varia a seconda della direzione del campo elettrico rispetto al mezzo, essa è rappresentata attraverso un tensore, che è una descrizione locale funzione delle coordinate del punto e indipendente dalla scelta del sistema di riferimento. Solo in particolari condizioni - ovvero nel caso si consideri un materiale lineare, omogeneo e isotropo - tutte le componenti del tensore hanno lo stesso valore e la permittività può essere trattata come uno scalare, chiamato impropriamente costante dielettrica.
La permittività di un materiale varia anche a seconda della frequenza del campo elettrico. Per descrivere tale dipendenza si utilizza una funzione complessa della frequenza, attraverso la quale è possibile trattare la propagazione del campo elettromagnetico in mezzi dissipativi (cioè a conducibilità finita) o dispersivi (cioè le cui proprietà elettromagnetiche variano al variare della frequenza dei campi incidenti). Il valore in una data direzione della permittività è quindi un numero complesso, che permette di descrivere la proporzionalità e lo sfasamento fra la polarizzazione nel dielettrico e il campo esterno forzante.
Quando si analizza la permittività dal punto di vista della frequenza del campo si nota che essa può presentare un comportamento anomalo in corrispondenza di certe lunghezze d'onda. Infatti, la parte immaginaria della permittività elettrica segue un andamento risonante in corrispondenza dei suoi poli, dove presenta uno o più picchi. In corrispondenza di questi picchi l'assorbimento da parte del materiale dell'energia posseduta dal campo è massimo.
Definizione |
Il vettore induzione elettrica D{displaystyle mathbf {D} }
La permittività elettrica ε{displaystyle varepsilon }
- D=εE{displaystyle mathbf {D} =varepsilon mathbf {E} }
Si tratta di una grandezza che dipende in generale da diversi parametri, tra i quali la posizione nel mezzo, la frequenza del campo applicato, la temperatura o l'umidità. In particolare, se il materiale è omogeneo e anisotropo la costante dielettrica diventa una matrice; se non è omogeneo i coefficienti della matrice sono una funzione della posizione, e se non è lineare la costante dielettrica dipende dal campo elettrico, ed in generale anche dal tempo. Se la permittività elettrica dipende dalla frequenza il mezzo si dice dispersivo.[3]
Nel caso in cui il mezzo sia lineare, omogeneo e isotropo, ponendo che la sua risposta all'applicazione del campo sia istantanea, la permittività elettrica è uno scalare. Se il materiale non è isotropo la permittività elettrica è un tensore del secondo ordine.
La permittività elettrica si misura in farad al metro nel SI:
- Fm=C2m⋅J=C2m2⋅N=A2⋅s4m3⋅kg{displaystyle mathrm {{frac {F}{m}}={frac {C^{2}}{mcdot J}}={frac {C^{2}}{m^{2}cdot N}}={frac {A^{2}cdot s^{4}}{m^{3}cdot kg}}} }
Permittività elettrica relativa |
.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}
La maggior parte dei materiali isolanti può essere trattata come un dielettrico lineare omogeneo ed isotropo; questo significa che tra il dipolo indotto nel materiale ed il campo elettrico esterno sussiste una relazione lineare. Si tratta di un'approssimazione di largo utilizzo, ed in tal caso i campi E{displaystyle mathbf {E} }
- D=ε0E+P=ε0(1+χ)E=εrε0E=εE{displaystyle mathbf {D} =varepsilon _{0}mathbf {E} +mathbf {P} =varepsilon _{0}(1+chi )mathbf {E} =varepsilon _{r}varepsilon _{0}mathbf {E} =varepsilon mathbf {E} }
Il numero ε0{displaystyle varepsilon _{0}}
- ε0=1c2μ0≈8,8541878176⋅10−12 Fm{displaystyle varepsilon _{0}={frac {1}{{c}^{2}mu _{0}}}approx 8{,}8541878176cdot 10^{-12} mathrm {frac {F}{m}} }
dove c{displaystyle c}
Il numero εr{displaystyle varepsilon _{r}}
Come conseguenza si ha:
- P=(εr−1)ε0E=ε0χE{displaystyle mathbf {P} =(varepsilon _{r}-1)varepsilon _{0}mathbf {E} =varepsilon _{0}chi mathbf {E} }
La suscettività è quindi legata alla permittività relativa εr{displaystyle varepsilon _{r}}
- χ=εr−1{displaystyle chi =varepsilon _{r}-1}
(che nel vuoto diventa χ=0{displaystyle chi =0}
Nel dominio delle frequenze, per un mezzo lineare e indipendente dal tempo sussiste la relazione:
- D(ν)=ε(ν)E(ν){displaystyle mathbf {D(nu )} =varepsilon (nu )mathbf {E} (nu )}
dove ν{displaystyle nu }
La velocità di fase v=cn{displaystyle v={c over n}}
- εμ=1v2{displaystyle varepsilon mu ={frac {1}{v^{2}}}}
Nel caso dell'aria, la permittività elettrica è εr=1,00059{displaystyle varepsilon _{r}=1{,}00059}
Modello per la permittività elettrica |
In un dielettrico perfetto per descrivere la formazione di un dipolo elettrico si assume che le cariche e{displaystyle e}
- F=−mω02x=−eE{displaystyle mathbf {F} =-momega _{0}^{2}mathbf {x} =-emathbf {E} }
dove ω0{displaystyle omega _{0}}
- p=ex=e2mω02E{displaystyle mathbf {p} =emathbf {x} ={frac {e^{2}}{momega _{0}^{2}}}mathbf {E} }
Si consideri ora un dielettrico non ideale ed un campo elettrico E(x,t){displaystyle mathbf {E} (mathbf {x} ,t)}
- F=mx¨=−mγx˙−mω02x−eE(x,t){displaystyle mathbf {F} =m{ddot {mathbf {x} }}=-mgamma {dot {mathbf {x} }}-momega _{0}^{2}mathbf {x} -emathbf {E} (mathbf {x} ,t)}
e l'equazione del moto assume pertanto la forma:[5]
- m[x¨+γx˙+ω02x]=−eE(x,t){displaystyle m[{ddot {mathbf {x} }}+gamma {dot {mathbf {x} }}+omega _{0}^{2}mathbf {x} ]=-emathbf {E} (mathbf {x} ,t)}
![m [ddot mathbf x + gamma dot mathbf x + omega_0^2 mathbf x ] = - e mathbf E (mathbf x , t)](https://wikimedia.org/api/rest_v1/media/math/render/svg/27b9e2171aaf1155a297b4bf43966ca667dd60a7)
Grazie alla dipendenza eiωt{displaystyle e^{iomega t}}
- x=em(ω02−ω2−iωγ)E{displaystyle mathbf {x} ={frac {e}{m(omega _{0}^{2}-omega ^{2}-iomega gamma )}}mathbf {E} }
Quindi il momento di dipolo per il singolo elettrone è dato da:
- p=−ex=e2m(ω02−ω2−iωγ)E{displaystyle mathbf {p} =-emathbf {x} ={frac {e^{2}}{m(omega _{0}^{2}-omega ^{2}-iomega gamma )}}mathbf {E} }
Si supponga vi siano N{displaystyle N}
- D=ε(ω)E=ε0E+ε0χE=ε0E+P=ε0E+Np{displaystyle mathbf {D} =varepsilon (omega )mathbf {E} =varepsilon _{0}mathbf {E} +varepsilon _{0}chi mathbf {E} =varepsilon _{0}mathbf {E} +mathbf {P} =varepsilon _{0}mathbf {E} +Nmathbf {p} }
dove χ{displaystyle chi }
- ε(ω)ε0=1+χ=1+Ne2ε0m∑jfjωj2−ω2−iωjγ{displaystyle {frac {varepsilon (omega )}{varepsilon _{0}}}=1+chi =1+{frac {Ne^{2}}{varepsilon _{0}m}}sum _{j}{frac {f_{j}}{omega _{j}^{2}-omega ^{2}-iomega _{j}gamma }}}
con:
- ∑jfj=Z{displaystyle sum _{j}f_{j}=Z}
Si nota che nei materiali conduttori la frequenza ω=0{displaystyle omega =0}
Il modello sviluppato permette di distinguere due tipologie di dispersione:
- Si definisce dispersione normale la dispersione in una regione dello spettro lontana dalle frequenze di risonanza, in cui la parte reale di ε(ω){displaystyle varepsilon (omega )}
.
- Si definisce dispersione anomala la dispersione in prossimità dalle frequenze di risonanza, in cui la parte reale di ε(ω){displaystyle varepsilon (omega )}
di ε(ω){displaystyle varepsilon (omega )}
Si verifica talvolta che ℑ(ε)<0{displaystyle Im (varepsilon )<0}
La dipendenza della permittività elettrica dalla frequenza del campo è rilevante quando la relativa lunghezza d'onda ha lo stesso ordine di grandezza dell'ampiezza dell'oscillazione delle cariche. Nei materiali dielettrici, pertanto, la polarizzazione avviene solitamente a partire da lunghezze d'onda confrontabili con la dimensione atomica o molecolare, che corrispondono alla regione dello spettro al di sotto del visibile. Nei conduttori, invece, le oscillazioni compiute dagli elettroni liberi sono di ampiezza maggiore poiché non vengono smorzate dalla vicinanza dei nuclei, e la modellizzazione della permittività elettrica diventa più elaborata.
Dispersione e causalità |
La polarizzazione di un materiale in risposta ad un campo elettrico non è in generale istantanea. Il fatto che la permittività elettrica dipenda dalla frequenza implica che la relazione tra i campi E{displaystyle mathbf {E} }
- D(x,ω)=ε(ω)E(x,ω){displaystyle mathbf {D} (mathbf {x} ,omega )=varepsilon (omega )mathbf {E} (mathbf {x} ,omega )}
è temporalmente non-locale. Considerando la rappresentazione per mezzo della trasformata di Fourier:
- D(x,t)=12π∫−∞∞D(x,ω)e−iωtdωD(x,ω)=12π∫−∞∞D(x,t′)eiωt′dt′{displaystyle mathbf {D} (mathbf {x} ,t)={frac {1}{sqrt {2pi }}}int _{-infty }^{infty }mathbf {D} (mathbf {x} ,omega )e^{-iomega t}domega qquad mathbf {D} (mathbf {x} ,omega )={frac {1}{sqrt {2pi }}}int _{-infty }^{infty }mathbf {D} (mathbf {x} ,t')e^{iomega t'}dt'}
ed inserendola nella precedente relazione, si ottiene:
- D(x,t)=12π∫−∞∞ε(ω)E(x,ω)e−iωtdω{displaystyle mathbf {D} (mathbf {x} ,t)={frac {1}{sqrt {2pi }}}int _{-infty }^{infty }varepsilon (omega )mathbf {E} (mathbf {x} ,omega )e^{-iomega t}domega }
Inserendo in tale espressione l'analoga rappresentazione di Fourier per E{displaystyle mathbf {E} }
- D(x,t)=12π∫−∞∞ε(ω)e−iωtdω∫−∞∞E(x,t′)eiωt′dt′{displaystyle mathbf {D} (mathbf {x} ,t)={frac {1}{2pi }}int _{-infty }^{infty }varepsilon (omega )e^{-iomega t}domega int _{-infty }^{infty }mathbf {E} (mathbf {x} ,t')e^{iomega t'}dt'}
Ponendo che si possa invertire l'ordine di integrazione:[7]
- D(x,t)=ε0[E(x,t)+∫−∞∞χ(t′)E(x,t−t′)dt′]{displaystyle mathbf {D} (mathbf {x} ,t)=varepsilon _{0}left[mathbf {E} (mathbf {x} ,t)+int _{-infty }^{infty }chi (t')mathbf {E} (mathbf {x} ,t-t')dt'right]}
![mathbf D (mathbf x , t) = varepsilon_0 left[ mathbf E (mathbf x , t) + int_{-infty}^{infty} chi(t') mathbf E (mathbf x , t-t')dt' right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d936e4fbab21e5eb7609304dfaf508b6ea33e033)
dove χ(t′){displaystyle chi (t')}
- χ(t′)=12π∫−∞∞χ(ω)e−iωt′dω=12π∫−∞∞(ε(ω)ε0−1)e−iωt′dω{displaystyle chi (t')={frac {1}{2pi }}int _{-infty }^{infty }chi (omega )e^{-iomega t'}domega ={frac {1}{2pi }}int _{-infty }^{infty }left({frac {varepsilon (omega )}{varepsilon _{0}}}-1right)e^{-iomega t'}domega }
I campi D{displaystyle mathbf {D} }
Suscettività elettrica |
Si consideri un modello per la permittività elettrica in cui vi sia una sola frequenza di risonanza. In accordo con la descrizione di ε(ω){displaystyle varepsilon (omega )}
- ε(ω)ε0=1+χe=1+ωp2ω02−ω2−iωjγ{displaystyle {frac {varepsilon (omega )}{varepsilon _{0}}}=1+chi _{e}=1+{frac {omega _{p}^{2}}{omega _{0}^{2}-omega ^{2}-iomega _{j}gamma }}}
La trasformata della suscettività elettrica assume in tal caso la forma:[8]
- χ(t′)=ωp22π∫−∞∞e−iωt′ω02−ω2−iωjγdω=ωp2e−γt′2sin(ν0t′)ν0θ(t′){displaystyle chi (t')={frac {omega _{p}^{2}}{2pi }}int _{-infty }^{infty }{frac {e^{-iomega t'}}{omega _{0}^{2}-omega ^{2}-iomega _{j}gamma }}domega =omega _{p}^{2}e^{-{frac {gamma t'}{2}}}{frac {sin(nu _{0}t')}{nu _{0}}}theta (t')}
dove θ(t′){displaystyle theta (t')}
- ν02=ω02−γ24{displaystyle nu _{0}^{2}=omega _{0}^{2}-{frac {gamma ^{2}}{4}}}
La funzione χ(t′){displaystyle chi (t')}
Si giunge in questo modo all'espressione più generale che lega i campi D{displaystyle mathbf {D} }
- D(x,t)=ε0[E(x,t)+∫0∞χ(t′)E(x,t−t′)dt′]{displaystyle mathbf {D} (mathbf {x} ,t)=varepsilon _{0}left[mathbf {E} (mathbf {x} ,t)+int _{0}^{infty }chi (t')mathbf {E} (mathbf {x} ,t-t')dt'right]}
![mathbf D (mathbf x , t) = varepsilon_0 left[ mathbf E (mathbf x , t) + int_{0}^{infty} chi(t') mathbf E (mathbf x , t-t')dt' right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bf1b65b9948c56a1f79320b6521647bbfaef9cc)
dove l'integrazione avviene a partire da t′=0{displaystyle t'=0}
Permittività complessa |
Spettro in frequenza della permittività elettrica dell'aria, in cui ε′{displaystyle varepsilon '}
è la parte reale, che caratterizza l'energia immagazzinata nel mezzo, mentre ε″{displaystyle varepsilon ''}
è la parte immaginaria, e descrive la dissipazione di energia nel mezzo. Si evidenziano sistemi fisici che ne determinano l'andamento in corrispondenza del rispettivo range di frequenze caratteristico.[10]La permittività elettrica è espressa attraverso la relazione:
- ε(ω)ε0=1+∫0∞χ(t′)eiωt′dt′{displaystyle {frac {varepsilon (omega )}{varepsilon _{0}}}=1+int _{0}^{infty }chi (t')e^{iomega t'}dt'}
dalla quale si evince che se la suscettività è finita ad ogni tempo e si annulla ad un tempo infinito, allora la permittività elettrica è una funzione analitica nel semipiano superiore del piano complesso.
Il fatto che in seguito all'applicazione di un campo elettrico la polarizzazione elettrica non sia istantanea, e che pertanto la risposta del mezzo dipenda dalla frequenza del campo, viene espresso attraverso una differenza di fase tra il campo e la risposta del materiale. La dipendenza dalla frequenza motiva pertanto il fatto che la permittività sia descritta da una funzione complessa ε^(ω){displaystyle {widehat {varepsilon }}(omega )}
- D0e−iωt=ε^(ω)E0e−iωt{displaystyle D_{0}e^{-iomega t}={widehat {varepsilon }}(omega )E_{0}e^{-iomega t}}
dove D0{displaystyle D_{0}}
- εs=limω→0ε^(ω){displaystyle varepsilon _{text{s}}=lim _{omega rightarrow 0}{widehat {varepsilon }}(omega )}
Mentre la permittività statica consente una buona approssimazione per basse frequenze del campo, al crescere della frequenza lo sfasamento δ{displaystyle delta }
- ε^=D0E0=|ε|eiδε^(ω)=D0E0(cosδ+isinδ){displaystyle {widehat {varepsilon }}={frac {D_{0}}{E_{0}}}=|varepsilon |e^{idelta }qquad {widehat {varepsilon }}(omega )={frac {D_{0}}{E_{0}}}left(cos delta +isin delta right)}
La funzione ε^(ω){displaystyle {widehat {varepsilon }}(omega )}
- ℜ[ε(ω)ε0]=1+1πP∫−∞∞ℑ(ε(ω′)ε0)ω′−ωdω′ℑ[ε(ω)ε0]=−1πP∫−∞∞ℜ(ε(ω′)ε0)−1ω′−ωdω′{displaystyle Re left[{frac {varepsilon (omega )}{varepsilon _{0}}}right]=1+{frac {1}{pi }}{mathcal {P}}int _{-infty }^{infty }{frac {Im left({frac {varepsilon (omega ')}{varepsilon _{0}}}right)}{omega '-omega }}domega 'qquad Im left[{frac {varepsilon (omega )}{varepsilon _{0}}}right]=-{frac {1}{pi }}{mathcal {P}}int _{-infty }^{infty }{frac {Re left({frac {varepsilon (omega ')}{varepsilon _{0}}}right)-1}{omega '-omega }}domega '}
![Re left[frac{varepsilon (omega)}{varepsilon_0} right] = 1 + frac{1}{pi} mathcal{P} int_{-infty}^{infty}frac{Im left(frac{varepsilon (omega')}{varepsilon_0} right)}{omega' - omega} domega' qquad Im left[frac{varepsilon (omega)}{varepsilon_0} right] = - frac{1}{pi} mathcal{P} int_{-infty}^{infty}frac{Re left( frac{varepsilon (omega')}{varepsilon_0}right) - 1 }{omega' - omega} domega'](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1c54d06b5a116701c5e5846bd6134ab519b90d)
dove P{displaystyle {mathcal {P}}}
Nei solidi, la funzione dielettrica ottica è data da:[12]
- ε(ω)=1+8π2e2m2∑c,v∫Wc,v(E)[φ(ℏω−E)−φ(ℏω+E)]dx{displaystyle varepsilon (omega )=1+{frac {8pi ^{2}e^{2}}{m^{2}}}sum _{c,v}int W_{c,v}(E)left[varphi (hbar omega -E)-varphi (hbar omega +E)right],dx}
![varepsilon(omega)=1+frac{8pi^2e^2}{m^2}sum_{c,v}int W_{c,v}(E) left[ varphi (hbar omega - E)-varphi( hbar omega +E) right ] , dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/5561a9792b50371664c8b31a2633611c86d6487e)
dove Wc,v(E){displaystyle W_{c,v}(E)}
Polarizzazione |
Il vettore di polarizzazione risulta essere una funzione dipendente dal tempo:
- P(t)=ε0∫−∞tχ(t−t′)E(t′)dt′{displaystyle mathbf {P} (t)=varepsilon _{0}int _{-infty }^{t}chi (t-t')mathbf {E} (t'),dt'}
Tale definizione è generale, in quanto tiene conto della non-località della relazione tra P{displaystyle mathbf {P} }
- χ(t−t′)=0t−t′<0{displaystyle chi (t-t')=0qquad t-t'<0}
Una risposta isantanea corrisponde matematicamente alla delta di Dirac:
- χ(t−t′)=χδ(t−t′){displaystyle chi (t-t')=chi delta (t-t')}
In un sistema lineare è conveniente considerare la trasformata di Fourier e scrivere la precedente relazione nel dominio della frequenza, nel quale per il teorema di convoluzione il prodotto di convoluzione di due funzioni viene espresso con il prodotto semplice delle rispettive trasformate:
- P(ω)=ε0χ(ω)E(ω){displaystyle mathbf {P} (omega )=varepsilon _{0}chi (omega )mathbf {E} (omega )}
La dipendenza dalla frequenza della suscettività determina la dipendenza dalla frequenza della permittività, e l'andamento della suscettività rispetto alla frequenza caratterizza le proprietà dispersive del materiale.
Importanza in chimica |
.mw-parser-output .avviso .mbox-text-div>div,.mw-parser-output .avviso .mbox-text-full-div>div{font-size:90%}.mw-parser-output .avviso .mbox-image div{width:52px}.mw-parser-output .avviso .mbox-text-full-div .hide-when-compact{display:block}
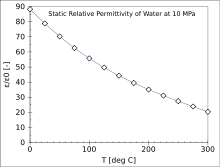
Dipendenza della permittività elettrica relativa (statica, frequenza tendente a 0) dell'acqua in funzione della temperatura, a pressione costante di 10 MPa (assoluta)
In chimica, particolarmente importante risulta la valutazione della permittività elettrica che caratterizza un dato solvente, in quanto questa grandezza permette di stabilire quale solvente sia più opportuno per portare in soluzione un dato soluto. Ad esempio, l'acqua è uno dei solventi polari che possiede permittività elettrica relativa molto elevata (78.5) ed è perciò in grado di solubilizzare i composti ionici o fortemente polari. Solo alcuni acidi acquosi molto forti possiedono una permittività elettrica superiore all'acqua es: acido nitrico, acido perclorico, acido tricloro- o trifluoroacetico. Di contro il benzene, con valore della costante dielettrica relativa 2.30, risulta un solvente molto utile per ottenere soluzioni di composti organici poco polari (o apolari) e non idrosolubili. L'etanolo è un solvente con caratteristiche intermedie, possedendo εr{displaystyle varepsilon _{r}}
La costante dielettrica di un solvente non è utile solamente nello studio della solubilità, ma risulta anche un importante parametro nella trattazione di processi elettrochimici, quale ad esempio l'elettroforesi, o nella trattazione termodinamica dei colloidi.
Note |
^ vedi dizionario Hoepli o Treccani
^ (EN) IUPAC Gold Book, "permittivity"
^ Jackson, Pag. 323
^ Mencuccini, Silvestrini, Pag. 143
^ Jackson, Pag. 309
^ Jackson, Pag. 310
^ Jackson, Pag. 330
^ Jackson, Pag. 331
^ Jackson, Pag. 332
^ Dielectric Spectroscopy Archiviato il 7 marzo 2001 in Internet Archive.
^ Jackson, Pag. 334
^
Peter Y. Yu, Manuel Cardona, Fundamentals of Semiconductors: Physics and Materials Properties, Berlin, Springer, 2001, p. 261, ISBN 3-540-25470-6.
^
José García Solé, Jose Solé, Luisa Bausa,, An introduction to the optical spectroscopy of inorganic solids, Wiley, 2001, Appendix A1, pp, 263, ISBN 0-470-86885-6.
^
John H. Moore, Nicholas D. Spencer, Encyclopedia of chemical physics and physical chemistry, Taylor and Francis, 2001, p. 105, ISBN 0-7503-0798-6.
^
Solé, José García, Bausá, Louisa E e Jaque, Daniel, Solé and Bausa, 22 marzo 2005, p. 10, ISBN 3-540-25470-6.
^
Hartmut Haug, Stephan W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, World Scientific, 1994, p. 196, ISBN 981-02-1864-8.
^
Manijeh Razeghi, Fundamentals of Solid State Engineering, Birkhauser, 2006, p. 383, ISBN 0-387-28152-5.
Bibliografia |
- Corrado Mencuccini, Vittorio Silvestrini, Fisica II, Napoli, Liguori Editore, 2010, ISBN 978-88-207-1633-2.
- (EN) John D Jackson, Classical Electrodynamics, 3rd Edition, Wiley, 1999, ISBN 0-471-30932-X.
- (EN) Landolt e Bornstein Landolt-Börnstein physikalisch-chemische tabellen (Berlino, Springer, 1912) (costanti dielettriche pp. 1211–1222)
- (EN) A. Von Hippel Tables of Dielectric Materials. (Massachusetts Institute of Technology, TR-94-4125, 1944)
- (EN) A. A. Maryott, ed E. R. Smith, Table of Dielectric Constants of Pure Liquids. (US National Bureau of Standards, 1951)
- (EN) A. Von Hippel .mw-parser-output .chiarimento{background:#ffeaea;color:#444444}.mw-parser-output .chiarimento-apice{color:red}
Tables of dielectric materials. Volume IV.[collegamento interrotto] (Massachusetts Institute of Technology, TR-57, 1953) - (EN) A. Von Hippel e W. B. Westphal Tables of Dielectric Materials. Volume 5. (Massachusetts Institute of Technology, TR-94-4124, 1957)
Voci correlate |
- Analisi termica dielettrica
- Assorbimento (ottica)
- Campo elettrico
- Dispersione ottica
- Equazione di Clausius-Mossotti
- Equazioni di Maxwell
- Forze di Van der Waals
- Induzione elettrica
- Isolante elettrico
- Legame idrogeno
- Permeabilità magnetica
- Polarizzabilità
- Polarizzazione elettrica
- Relazione di Kramers-Kronig
- Suscettività elettrica
- Trasformata di Fourier
Collegamenti esterni |
Permittività elettrica, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
(EN) Permittività elettrica, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- Costanti dielettriche relative, su itchiavari.org.
Portale Elettrochimica
Portale Elettromagnetismo
Portale Matematica
