Gfrktyl

Il teorema fondamentale dell'algebra asserisce che ogni polinomio di grado n≥1{displaystyle ngeq 1} (cioè non costante), su un campo algebricamente chiuso (come il campo dei numeri complessi), del tipo:

anzn+…+a1z+a0{displaystyle a_{n}z^{n}+ldots +a_{1}z+a_{0}}

ammette esattamente n{displaystyle n}radici in quel campo, o zeri. Dal teorema segue che un polinomio complesso ammette esattamente n{displaystyle n}radici complesse (contate con la giusta molteplicità), mentre un polinomio reale ammette al più n{displaystyle n}radici reali.

Storia |

Un'enunciazione del teorema in una pubblicazione fu opera del matematico di origine fiamminga Albert Girard nel 1629 nel libro L'invention en algebre, per quanto anticipata da una formulazione debole da parte di Peter Roth, riportata nei suoi Arithmetica Philosophica (1608).^[1] Non vi era comunque alcuna dimostrazione. Nel 1702 Leibniz sostenne di aver trovato un controesempio con il polinomio x4+1{displaystyle x^{4}+1}. Nel 1742 Nicolas Bernoulli e Christian Goldbach in una lettera inviata allo stesso Leibniz dimostrarono l'esistenza di radici complesse del polinomio.^[2]

Il primo tentativo serio di dimostrazione del teorema fu operato da d'Alembert nel 1746, il quale però utilizzò un teorema non ancora dimostrato (la dimostrazione fu fatta da Puiseux nel 1751 utilizzando lo stesso teorema fondamentale dell'algebra). Altri tentativi di dimostrazione furono portati avanti nel 1749 da Eulero, Lagrange nel 1772, Laplace nel 1795.

Finalmente nel 1799 Gauss riuscì nell'intento sfruttando i tentativi dei suoi predecessori. Infine, nel 1814 Jean-Robert Argand, un libraio appassionato di matematica, pubblicò un'altra dimostrazione molto più semplice rispetto a quella di Gauss.

Esempi |

Polinomi a coefficienti reali |

Un numero reale è un particolare numero complesso: il teorema è quindi valido per ogni polinomio a coefficienti reali. Ad esempio, si consideri il polinomio

p(z)=z2+1{displaystyle p(z)=z^{2}+1}

Questo polinomio non ammette nessuna radice reale: i numeri reali non formano un campo algebricamente chiuso. Per il teorema fondamentale dell'algebra, il polinomio ha però almeno una radice complessa: questa è l'unità immaginaria z=i{displaystyle z=i}. Infatti:

p(i)=i2+1=−1+1=0{displaystyle p(i)=i^{2}+1=-1+1=0}

Questa non è però l'unica radice. Il polinomio ha grado due e ha due radici complesse i{displaystyle i} e −i{displaystyle -i}.

Dimostrazioni |

Esistono numerose dimostrazioni del teorema fondamentale dell'algebra che coinvolgono settori molto diversi della matematica come la topologia, l'analisi complessa e l'algebra.

Dimostrazione basata sullo sviluppo in serie di Taylor |

Sia p(z){displaystyle p(z)} un polinomio a coefficienti complessi di grado n≥1{displaystyle ngeq 1}.

Abbiamo lim|z|→+∞|p(z)|=+∞{displaystyle lim _{|z|to +infty }|p(z)|=+infty }, quindi esiste r>0{displaystyle r>0} tale che

|p(z)|>|p(0)|{displaystyle |p(z)|>|p(0)|} per ogni z∈C{displaystyle zin mathbb {C} } tale che |z|>r{displaystyle |z|>r}.

Il disco chiuso Dr:={z∈C:|z|≤r}{displaystyle D_{r}:={zin mathbb {C} :|z|leq r}} è compatto, dunque per il teorema di Weierstrass esiste un punto z0∈Dr{displaystyle z_{0}in D_{r}} in cui |p(z)|{displaystyle |p(z)|} assume il suo minimo valore assoluto in Dr{displaystyle D_{r}}.

Proviamo che |p(z0)|=0{displaystyle |p(z_{0})|=0}: sviluppando p(z){displaystyle p(z)} in serie di Taylor intorno a z0{displaystyle z_{0}} abbiamo

∀z∈C:p(z)=a0+ak(z−z0)k+ak+1(z−z0)k+1+⋯+an(z−z0)n{displaystyle forall zin mathbb {C} ;:quad p(z)=a_{0}+a_{k}(z-z_{0})^{k}+a_{k+1}(z-z_{0})^{k+1}+cdots +a_{n}(z-z_{0})^{n}}

dove a0=p(z0){displaystyle a_{0}=p(z_{0})}, k≥1{displaystyle kgeq 1} è intero e ak,ak+1,…,an∈C{displaystyle a_{k},a_{k+1},ldots ,a_{n}in mathbb {C} } con ak≠0{displaystyle a_{k}neq 0},

notare che la serie di Taylor è finita poiché p(m)(z0)=0{displaystyle p^{(m)}(z_{0})=0} per ogni intero m>n{displaystyle m>n} essendo p(z){displaystyle p(z)} un polinomio di grado n{displaystyle n}. Quindi:

p(z)=a0+ak(z−z0)k+R(z){displaystyle p(z)=a_{0}+a_{k}(z-z_{0})^{k}+R(z)}

dove R(z)=o((z−z0)k){displaystyle R(z)=o((z-z_{0})^{k})} per z→z0{displaystyle zto z_{0}}.

Per ogni ε>0{displaystyle varepsilon >0} possiamo scegliere z∈C{displaystyle zin mathbb {C} } di modo che ak(z−z0)k=−εa0{displaystyle a_{k}(z-z_{0})^{k}=-varepsilon a_{0}}, in tal caso quando ε→0+{displaystyle varepsilon to 0^{+}} allora z→z0{displaystyle zto z_{0}} quindi per ε{displaystyle varepsilon } sufficientemente piccolo avremo

|R(z)|=|o((z−z0)εa0/ak)|<12εa0{displaystyle |R(z)|=|o((z-z_{0})varepsilon a_{0}/a_{k})|<{tfrac {1}{2}}varepsilon a_{0}}

pertanto

|p(z)|≤|(1−ε)a0|+|R(z)|<(1−12ε)|a0|<|p(z0)|{displaystyle |p(z)|leq |(1-varepsilon )a_{0}|+|R(z)|<(1-{tfrac {1}{2}}varepsilon )|a_{0}|<|p(z_{0})|}

ovvero si è trovato un assurdo.

Dimostrazione basata sull'analisi complessa |

Sia p(z){displaystyle p(z)} un polinomio complesso, tale che p(z)≠0{displaystyle p(z)neq 0} per ogni z{displaystyle z} complesso. Allora la funzione

f(z)=1p(z){displaystyle f(z)={frac {1}{p(z)}}}

è una funzione intera, cioè è una funzione olomorfa su tutto C{displaystyle mathbb {C} }. D'altra parte

lim|z|→+∞|p(z)|=+∞{displaystyle lim _{|z|to +infty }|p(z)|=+infty }

implica

lim|z|→+∞|f(z)|=0{displaystyle lim _{|z|to +infty }|f(z)|=0}

e quindi la funzione f(z){displaystyle f(z)} è limitata. Per il teorema di Liouville f(z){displaystyle f(z)} è costante, da cui segue che anche p(z){displaystyle p(z)} è costante.

Quindi gli unici polinomi senza zeri sono i polinomi costanti.

Dimostrazione topologica |

Consideriamo un polinomio a coefficienti complessi non costante

P(z)=anzn+an−1zn−1+…+a1z+a0{displaystyle P(z)=a_{n}z^{n}+a_{n-1}z^{n-1}+ldots +a_{1}z+a_{0}}

vogliamo dimostrare che esiste un punto α{displaystyle alpha } tale che P(α)=0{displaystyle P(alpha )=0}. A tale scopo possiamo considerare il caso in cui an=1{displaystyle a_{n}=1}.

Supponiamo per assurdo che P{displaystyle P} non ammetta radici, cioè che l'origine non sia nella sua immagine. Consideriamo sul piano complesso la circonferenza di centro l'origine e raggio r{displaystyle r} parametrizzata da

γr(t)=reit{displaystyle gamma _{r}(t)=re^{it}}

Il polinomio P{displaystyle P} rappresenta una funzione continua del piano complesso in sé stesso e come tale manderà la circonferenza γr{displaystyle gamma _{r}} in una curva piana parametrizzata P(γr){displaystyle P(gamma _{r})}. La curva così ottenuta non passerà per l'origine dal momento che abbiamo assunto che 0 non è nell'immagine di P{displaystyle P}, e questo qualunque sia il raggio r{displaystyle r}. Quindi possiamo considerare l'indice di avvolgimento di P(γr){displaystyle P(gamma _{r})} rispetto all'origine I(P(γr),0){displaystyle I(P(gamma _{r}),0)}

Poniamo

Φ(r)=I(P(γr),0),!{displaystyle Phi (r)=I(P(gamma _{r}),0),,!}

Poiché l'indice di avvolgimento non varia per deformazioni della curva tali che questa non tocchi mai l'origine (è un invariante omotopico) la funzione Φ(r){displaystyle Phi (r)} sarà continua e poiché l'indice assume solo valori interi dovrà anche essere una funzione costante.

Ora consideriamo il valore di Φ(r){displaystyle Phi (r)} per due differenti valori di r{displaystyle r}:

• per r=0{displaystyle r=0} la curva γr{displaystyle gamma _{r}} è costituita da un unico punto (l'origine) e la sua immagine sarà quindi anch'essa un unico punto che non può essere l'origine. In questo caso evidentemente si ha che I(P(γ0),0)=Φ(0)=0{displaystyle I(P(gamma _{0}),0)=Phi (0)=0}.


• per r{displaystyle r} abbastanza grandi affinché si abbia
  

  r>1,r>|an−1|+...+|a0|{displaystyle r>1,quad r>|a_{n-1}|+...+|a_{0}|}

  
  

abbiamo che la curva P(γr){displaystyle P(gamma _{r})} può essere deformata con continuità nella curva γrn{displaystyle gamma _{r}^{n}} definita da

t↦rneint{displaystyle tmapsto r^{n}e^{int}}

immagine di γr{displaystyle gamma _{r}} mediante la funzione polinomiale zn{displaystyle z^{n}}. Poiché l'indice di questa curva rispetto all'origine è n{displaystyle n} e per l'invarianza omotopica possiamo dedurre che Φ(r)=n{displaystyle Phi (r)=n}.

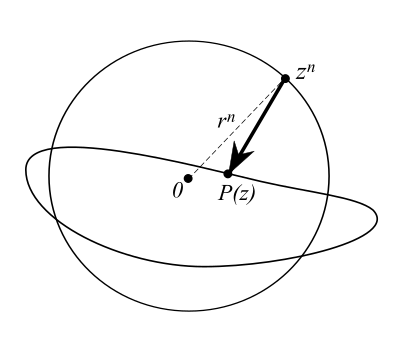
Per dimostrare questo osserviamo che finché z{displaystyle z} si trova nella circonferenza |z|=r{displaystyle |z|=r} vale la seguente catena di disuguaglianze:

|P(z)−zn|=|an−1zn−1+...+a1z+a0|{displaystyle |P(z)-z^{n}|=|a_{n-1}z^{n-1}+...+a_{1}z+a_{0}|}

≤|an−1||z|n−1+...+|a1||z|+|a0|{displaystyle leq |a_{n-1}||z|^{n-1}+...+|a_{1}||z|+|a_{0}|}

=|an−1|rn−1+...+|a1|r+|a0|{displaystyle =|a_{n-1}|r^{n-1}+...+|a_{1}|r+|a_{0}|}

<rn−1(|an−1|+...+|a1|+|a0|){displaystyle <r^{n-1}(|a_{n-1}|+...+|a_{1}|+|a_{0}|)}

<rn−1⋅r=rn=|zn|{displaystyle <r^{n-1}cdot r=r^{n}=|z^{n}|}

questo significa che fintanto che z{displaystyle z} si trova sulla circonferenza di raggio r{displaystyle r} la distanza che separa il punto P(z){displaystyle P(z)} della curva immagine dal punto zn{displaystyle z^{n}} è minore di quella che separa il punto zn{displaystyle z^{n}} dall'origine, dunque il segmento che congiunge P(z){displaystyle P(z)} a zn{displaystyle z^{n}} non tocca l'origine per ogni z{displaystyle z} in γr{displaystyle gamma _{r}} e questo permette di definire una deformazione continua di P(γr){displaystyle P(gamma _{r})} in γrn{displaystyle gamma _{r}^{n}} che non faccia passare la curva per l'origine.

Il fatto che Φ(r){displaystyle Phi (r)} assuma valori differenti per differenti raggi contraddice il fatto che deve essere una funzione costante, e siamo quindi giunti a un assurdo da cui concludiamo che l'ipotesi che P{displaystyle P} non avesse nessuna radice è impossibile.

Campi algebricamente chiusi |

.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}

Lo stesso argomento in dettaglio: Campo algebricamente chiuso.

Si dice che il campo complesso C{displaystyle mathbb {C} } è un campo algebricamente chiuso per indicare il fatto che
ogni polinomio di grado maggiore o uguale a 1, a coefficienti complessi, ha almeno una radice in C{displaystyle mathbb {C} }, come stabilisce il teorema qui esposto. Tale proprietà non è condivisa dai sottocampi Q{displaystyle mathbb {Q} } e R{displaystyle mathbb {R} } come si può vedere subito considerando i polinomi

x2−2{displaystyle x^{2}-2}

che non ha radici nel campo Q{displaystyle mathbb {Q} } dei razionali, e

x2+1{displaystyle x^{2}+1}

che non ha radici nel campo R{displaystyle mathbb {R} } dei reali.

Note |

Voci correlate |

• Teoria di Galois

Altri progetti |

• 
  Wikimedia Commons contiene immagini o altri file su teorema fondamentale dell'algebra
  

Collegamenti esterni |

• 
  


• 
  Teorema fondamentale dell'algebra, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
  


• 
  (EN) Teorema fondamentale dell'algebra, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
  

.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}

V · D · M Algebra
Numeri	Naturali · Interi · Razionali · Irrazionali · Algebrici · Trascendenti · Reali · Complessi
Principi fondamentali	Principio d'induzione · Principio del buon ordinamento · Relazione di equivalenza · Relazione d'ordine
Elementi di Calcolo combinatorio	Fattoriale · Permutazione · Disposizione · Combinazione · Dismutazione · Principio di inclusione-esclusione
Concetti fondamentali di Teoria dei numeri	Primi Numero primo · Teorema dell'infinità dei numeri primi · Crivello di Eratostene · Crivello di Atkin · Test di primalità · Teorema fondamentale dell'aritmetica Divisori Interi coprimi · Identità di Bézout · MCD · mcm · Algoritmo di Euclide · Criteri di divisibilità · Divisore Aritmetica modulare Teorema cinese del resto · Piccolo teorema di Fermat · Teorema di Eulero · Funzione φ di Eulero · Teorema di Wilson · Reciprocità quadratica
Algebra elementare	Equazione · Disequazione · Polinomio · Triangolo di Tartaglia · Teorema binomiale · Teorema del resto · Lemma di Gauss · Teorema delle radici razionali · Criterio di Eisenstein · Criterio di Cartesio
Teoria dei gruppi	Gruppi Gruppo (finito · ciclico · abeliano) · Gruppo primario · Gruppo quoziente · Gruppo nilpotente · Gruppo risolubile · Gruppo simmetrico · Gruppo diedrale · Gruppo semplice · Gruppo sporadico · Gruppo mostro · Gruppo di Klein · Gruppo dei quaternioni · Gruppo generale lineare · Gruppo ortogonale · Gruppo unitario · Gruppo unitario speciale · Gruppo residualmente finito · Gruppo spaziale · Prodotto diretto · Prodotto semidiretto Teoremi Teorema di isomorfismo · Teorema di Lagrange · Teorema di Cauchy · Teoremi di Sylow · Teorema di Cayley · Teorema di struttura dei gruppi abeliani finiti · Lemma della farfalla · Classificazione dei gruppi semplici finiti Sottoinsiemi Sottogruppo · Sottogruppo normale · Sottogruppo caratteristico · Sottogruppo di Frattini · Sottogruppo di torsione · Classe laterale · Classe di coniugio · Serie di composizione Omomorfismo · Isomorfismo · Automorfismo interno · Automorfismo esterno · Permutazione · Presentazione di un gruppo · Azione di gruppo
Teoria degli anelli	Anello (artiniano · noetheriano) · Caratteristica · Ideale (primo · massimale) · Dominio (a fattorizzazione unica · a ideali principali · euclideo) · Matrice · Anello semplice · Teorema di Artin-Wedderburn · Modulo · Dominio di Dedekind · Estensione di anelli · Teorema della base di Hilbert
Teoria dei campi	Campo · Polinomio irriducibile · Polinomio ciclotomico · Teorema fondamentale dell'algebra · Campo finito · Automorfismo · Endomorfismo di Frobenius Estensioni Campo di spezzamento · Estensione di campi · Estensione algebrica · Estensione separabile · Chiusura algebrica · Campo di numeri · Estensione normale · Estensione di Galois · Estensione abeliana · Estensione ciclotomica · Teoria di Kummer Teoria di Galois Gruppo di Galois · Teoria di Galois · Teorema fondamentale della teoria di Galois · Teorema di Abel-Ruffini · Costruzioni con riga e compasso
Altre strutture algebriche	Magma · Semigruppo · Corpo · Spazio vettoriale · Algebra su campo · Algebra di Lie · Algebra differenziale · Algebra di Clifford · Gruppo topologico · Gruppo ordinato · Quasi-anello

.mw-parser-output .CdA{border:1px solid #aaa;width:100%;margin:auto;font-size:90%;padding:2px}.mw-parser-output .CdA th{background-color:#ddddff;font-weight:bold;width:20%}

Controllo di autorità	GND (DE) 4155641-0

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica